题目内容
9.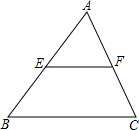 如图,△ABC中,E、F分别是AB、AC的中点,若△AEF的面积为1,则四边形EBCF的面积为3.
如图,△ABC中,E、F分别是AB、AC的中点,若△AEF的面积为1,则四边形EBCF的面积为3.
分析 根据三角形中位线定理得到EF∥BC,EF=$\frac{1}{2}$BC,得到△AEF∽△ABC,根据相似三角形的面积比等于相似比的平方计算即可.
解答 解:∵E、F分别是AB、AC的中点,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴△AEF∽△ABC,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=($\frac{1}{2}$)2,
∵△AEF的面积为1,
∴△ABC的面积为4,
∴四边形EBCF的面积为4-1=3,
故答案为:3.
点评 本题考查的是相似三角形的判定和性质、三角形中位线定理的应用,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列命题中是真命题的是( )
| A. | 所有的矩形都相似 | |
| B. | 所有的直角三角形都相似 | |
| C. | 有一个角是50°的所有等腰三角形都相似 | |
| D. | 有一个角是100°的所有等腰三角形都相似 |
17.某班学生军训射击,有m人各打中a环,n人各打中b环,那么该班打中a环和b环学生的平均环数是( )
| A. | $\frac{a+b}{m+n}$ | B. | $\frac{1}{2}$($\frac{a}{m}$+$\frac{b}{n}$) | C. | $\frac{am+bn}{m+n}$ | D. | $\frac{1}{2}$(am+bn) |
18.计算-0.32÷0.5×2÷(-2)3的结果是( )
| A. | $\frac{9}{100}$ | B. | -$\frac{9}{100}$ | C. | $\frac{9}{200}$ | D. | -$\frac{9}{200}$ |
19.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
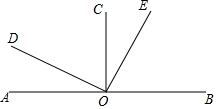 如图,己知直线AB上一点O,OC⊥AB,OD⊥OE,若∠COE=$\frac{1}{5}$∠BOD.
如图,己知直线AB上一点O,OC⊥AB,OD⊥OE,若∠COE=$\frac{1}{5}$∠BOD.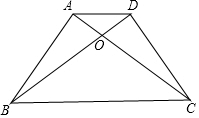 如图所示,AB⊥AC,DC⊥BD,AB=DC,求证:△ABD≌△DCA.
如图所示,AB⊥AC,DC⊥BD,AB=DC,求证:△ABD≌△DCA.