题目内容
3.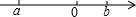 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )| A. | 2a+b | B. | 2a-b | C. | -2a+b | D. | b |
分析 根据点的坐标,可得a、b的关系,根据二次根式的性质,可化简二次根式,根据整式的加减,可得答案.
解答 解:由数轴上点的位置关系,得
a<b,|a|>|b|.
$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$=-a-(b-a)=a-b+a=2a-b,
故选:B.
点评 本题考查了实数与数轴,利用点的坐标得出a、b的关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.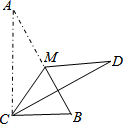 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
18.下列函数中,y是x的反比例函数有( )
(1)y=3x;(2)y=-$\frac{2}{x}$;(3)$y=\frac{x}{3}$;(4)-xy=3;(5)$y=\frac{2}{x+1}$;(6)$y=\frac{1}{x^2}$;(7)y=2x-2;(8)$y=\frac{k}{x}$.
(1)y=3x;(2)y=-$\frac{2}{x}$;(3)$y=\frac{x}{3}$;(4)-xy=3;(5)$y=\frac{2}{x+1}$;(6)$y=\frac{1}{x^2}$;(7)y=2x-2;(8)$y=\frac{k}{x}$.
| A. | (2)(4) | B. | (2)(3)(5)(8) | C. | (2)(7)(8) | D. | (1)(3)(4)(6) |
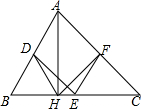 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.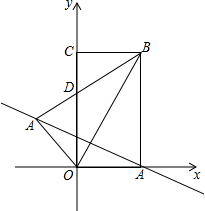 如图,矩形OABC在平面直角坐标系中,若OA,OC的长满足|OA-2|+(OC-2$\sqrt{3}$)2=0.
如图,矩形OABC在平面直角坐标系中,若OA,OC的长满足|OA-2|+(OC-2$\sqrt{3}$)2=0.