题目内容
9.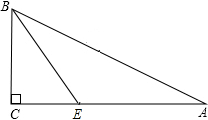 如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )| A. | 3 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 先由三角形内角和定理求出∠ABC的度数为60°,然后由BE平分∠ABC,可求∠ABE=∠CBE=30°,进而可得AE=BE,然后由∠A=30°,AB=12,可得BC=$\frac{1}{2}$AB=6,然后在Rt△BCE中,由30°角所对的直角边等于斜边的一半,可得CE=$\frac{1}{2}$BE,然后根据勾股定理求出BE的值,即可得到AE的长度.
解答 解:在三角形ABC中,∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=30°,
∴AE=BE,
∵∠A=30°,AB=12,
∴BC=$\frac{1}{2}$AB=6,
∵∠CBE=30°,
∴CE=$\frac{1}{2}$BE,
在Rt△BCE中,由勾股定理得:
BC2+CE2=BE2,
即:62+($\frac{1}{2}$BE)2=BE2,
解得:BE=4$\sqrt{3}$,
∴AE=4$\sqrt{3}$.
故选:C.
点评 本题考查了含30度角的直角三角形以及勾股定理的应用,解题的关键是:明确30度角所对的直角边等于斜边的一半.

练习册系列答案
相关题目
17.下列各式成立的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | $\sqrt{4+9}$=$\sqrt{4}$+$\sqrt{9}$ | C. | $\sqrt{3×9}$=$\sqrt{3}$×$\sqrt{9}$ | D. | $\sqrt{{x}^{2}}$=x |
1. 如图,点D在△ABC的边BC上,且CD=AD,则点D在( )的垂直平分线上.
如图,点D在△ABC的边BC上,且CD=AD,则点D在( )的垂直平分线上.
 如图,点D在△ABC的边BC上,且CD=AD,则点D在( )的垂直平分线上.
如图,点D在△ABC的边BC上,且CD=AD,则点D在( )的垂直平分线上.| A. | AB | B. | AC | C. | BC | D. | 不能确定 |
18.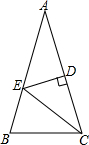 如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )
如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )
 如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )
如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
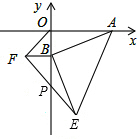 如图,点A的坐标为(8,0),点B是y轴负半轴上的任意一点,分别以OB,AB为直角边的第三第四象限作等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,则BP的长度为4.
如图,点A的坐标为(8,0),点B是y轴负半轴上的任意一点,分别以OB,AB为直角边的第三第四象限作等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,则BP的长度为4.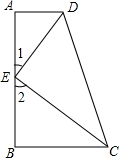 如图所示,AD⊥AB,DE,CE分别是∠ADC与∠BCD的平分线,∠1+∠2=90°,AD与BC平行吗?为什么?
如图所示,AD⊥AB,DE,CE分别是∠ADC与∠BCD的平分线,∠1+∠2=90°,AD与BC平行吗?为什么?
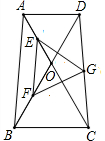 在梯形ABCD中,AD∥BC,AB=CD,∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由.
在梯形ABCD中,AD∥BC,AB=CD,∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由.