题目内容
18.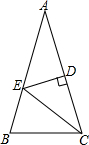 如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )
如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据∠A=36°,∠B=72°利用三角形内角和定理求出∠ACB=72°,故可得AB=AC,利用由DE垂直平分AB,求出∠ACE的度数,然后可得∠BEC=∠B,同理即可证明:△ABE,△BEC是等腰三角形.
解答 解:∵∠A=36°,∠B=72°,
∴∠ACB=180°-36°-72°=72°,
∴∠ACB=∠B,
∴AB=AC,
∴△ABC是等腰三角形,
∵DE垂直平分AC,
∴EA=EC,
∴∠ACE=∠A=36°.
∴AE=CE,
∴△ACE是等腰三角形,
∴∠AEC=180°-36°-36°=108°,
∴∠BEC=72°.
∴∠BEC=∠B,
∴CE=BC.
∴△BEC是等腰三角形,
∴等腰三角形有△ABC,△ACE,△BEC,
故选:B.
点评 本题主要考查等腰三角形的判定和性质,线段垂直平分线的性质,三角形的内角和定理,熟记有关的性质定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.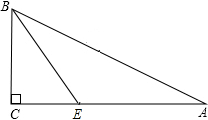 如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
 如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )| A. | 3 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |


 如图,AD是△ABC的中线,E是AD的中点,BE的延长线交AC于点F,若FC=12,AF的长为( )
如图,AD是△ABC的中线,E是AD的中点,BE的延长线交AC于点F,若FC=12,AF的长为( )