题目内容
7.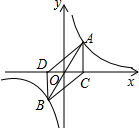 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )| A. | S=2 | B. | 2<S<4 | C. | S=4 | D. | S>4 |
分析 根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S=$\frac{1}{2}$|k|可知,S△AOC=S△BOD=$\frac{1}{2}$|k|,再根据反比例函数的对称性可知,O为DC中点,则S△AOD=S△AOC=$\frac{1}{2}$|k|,S△BOC=S△BOD=$\frac{1}{2}$|k|,进而求出四边形ADBC的面积.
解答 解:∵A,B是函数y=$\frac{2}{x}$的图象上关于原点O对称的任意两点,且AC垂直于x轴于点C,BD垂直于y轴于点D,
∴S△AOC=S△BOD=$\frac{1}{2}$×2=1,
假设A点坐标为(x,y),则B点坐标为(-x,-y),
则OC=OD=x,
∴S△AOD=S△AOC=1,S△BOC=S△BOD=1,
∴四边形ADBC面积=S△AOD+S△AOC+S△BOC+S△BOD=4.
故选C.
点评 本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
15. 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
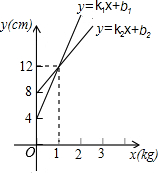 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
12.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )
| A. |  +4.5 | B. |  -1.5 | C. |  -0.4 | D. |  +0.6 |
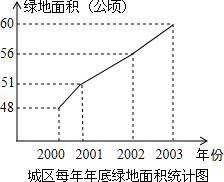 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).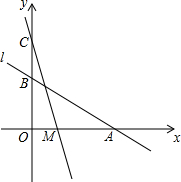 如图,直线L:y=-$\frac{1}{2}x+2$与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}x+2$与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.