题目内容
15.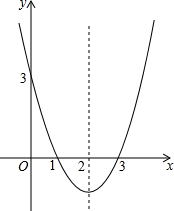 已知:抛物线y=ax2+bx+c的图象如图所示.
已知:抛物线y=ax2+bx+c的图象如图所示.(1)求这条抛物线所对应的二次函数的关系式;
(2)写出它的开口方向、对称轴和顶点坐标;
(3)这个函数有最大值还是最小值?这个值是多少?
(4)要使该二次函数的图象与x轴只有一个交点,应把该图象沿y轴向上平移几个单位?
分析 (1)根据图形得出三点坐标,代入抛物线解析式求出a,b,c的值,即可确定出解析式;
(2)利用二次函数的性质确定出开口方向,对称轴,以及顶点坐标即可;
(3)利用二次函数性质求出最值即可;
(4)利用平移规律得到结果即可.
解答 解:(1)根据题意得:(1,0);(3,0);(0,3)在抛物线上,
代入得:$\left\{\begin{array}{l}{a+b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$,
则抛物线解析式为y=x2-4x+3;
(2)∵a>0,
∴抛物线开口向上,
对称轴为直线x=2;顶点坐标为(2,-1);
(3)∵抛物线开口向上,
∴二次函数有最小值为-1;
(4)要使该二次函数的图象与x轴只有一个交点,应把该图象沿y轴向上平移1个单位.
点评 此题考查了待定系数法求抛物线解析式,二次函数图象与性质,以及二次函数与坐标轴的交点,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
5.$\sqrt{{{(-5)}^2}}$的算术平方根是( )
| A. | ±5 | B. | 5 | C. | -5 | D. | $\sqrt{5}$ |
7.下列条件中,能判定四边形是菱形的是( )
| A. | 对角线垂直 | B. | 两对角线相等 | ||
| C. | 两对线互相平分 | D. | 两对角线互相垂直平分 |
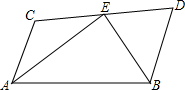 己知AC∥BD,∠CAB和∠DBA的平分线EA、EB与CD相交于点E,求证:CE=DE.
己知AC∥BD,∠CAB和∠DBA的平分线EA、EB与CD相交于点E,求证:CE=DE.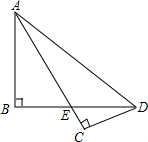 如图,AB⊥BD,垂足为B,AC⊥CD,垂足为C,且AC与BD交于点E,那么,
如图,AB⊥BD,垂足为B,AC⊥CD,垂足为C,且AC与BD交于点E,那么,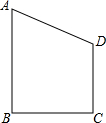 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,∠A=60°,BC=$\sqrt{3}$,DC=3,把直角梯形ABCD以AB所在的直线为轴旋转一周,求所得的几何体的全面积.
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,∠A=60°,BC=$\sqrt{3}$,DC=3,把直角梯形ABCD以AB所在的直线为轴旋转一周,求所得的几何体的全面积.