题目内容
5.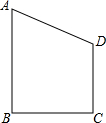 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,∠A=60°,BC=$\sqrt{3}$,DC=3,把直角梯形ABCD以AB所在的直线为轴旋转一周,求所得的几何体的全面积.
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,∠A=60°,BC=$\sqrt{3}$,DC=3,把直角梯形ABCD以AB所在的直线为轴旋转一周,求所得的几何体的全面积.
分析 作DE⊥AB于点E,求得AD的长,然后利用圆锥的侧面积的计算公式,圆柱的侧面积公式以及圆的面积公式即可求解.
解答  解:作DE⊥AB于点E.
解:作DE⊥AB于点E.
则AD=$\frac{DE}{sin60°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2.
所得的几何体的全面积是:2$\sqrt{3}$π×3+π($\sqrt{3}$)2+2$\sqrt{3}$π×2=6$\sqrt{3}$π+3π+4$\sqrt{3}$π=(10$\sqrt{3}$+3)π.
点评 本题考查圆锥的计算和圆柱的计算;得到几何体的形状是解决本题的突破点;需掌握圆锥、圆柱侧面积的计算公式.

练习册系列答案
相关题目
16.下列图案既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.已知三角形的三边长的比是2:3:4,则对应边上的高的比是( )
| A. | 3:4:6 | B. | 6:4:3 | C. | 2:3:4 | D. | 4:3:2 |
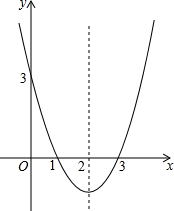 已知:抛物线y=ax2+bx+c的图象如图所示.
已知:抛物线y=ax2+bx+c的图象如图所示.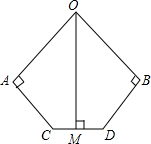 如图,OA=0B,AC=BD,0A⊥AC,0B⊥BD,OM⊥CD于M,求证:OM平分∠A0B.
如图,OA=0B,AC=BD,0A⊥AC,0B⊥BD,OM⊥CD于M,求证:OM平分∠A0B.