题目内容
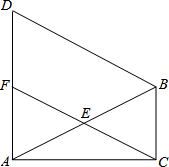
10．
如图所示，有一条宽相等的小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，若要硬化这条小路，且每平方米造价50元，则需要多少元钱？
分析 四边形ABCD是矩形，则AF∥EC，又AF=CE，进而可判断四边形AECF的形状，继而面积可以利用底边长乘以高进行计算．
解答 解：在矩形ABCD中，AF∥EC，
又∵AF=EC，
∴四边形AECF是平行四边形．
在Rt△ABE中，AB=60，AE=100，
根据勾股定理得BE=80，
∴EC=BC-BE=4，
所以这条小路的面积S=EC•AB=4×60=240（m2）．
240×50=1200元．
答：需要1200元钱．
点评 此题考查平移问题，关键是熟练掌握平行四边形的性质及判定，掌握矩形的性质及勾股定理．
练习册系列答案
相关题目
16．
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列五个结论中：①a+b+c＜0；②a-b+c＞0；③2a-b＜0；④abc＜0；⑤4a+2b+c＞0，错误的个数有（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列五个结论中：①a+b+c＜0；②a-b+c＞0；③2a-b＜0；④abc＜0；⑤4a+2b+c＞0，错误的个数有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE并延长交AD于F．求证：
5．
如图，OA⊥OB，等腰直角三角形CDE的腰CD在OB上，∠ECD=45°，将三角形CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则$\frac{OC}{CN}$的值为（ ）
如图，OA⊥OB，等腰直角三角形CDE的腰CD在OB上，∠ECD=45°，将三角形CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则$\frac{OC}{CN}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
如图，小虎在篮球场上玩，从点O出发，沿着O→A→B→O的路径匀速跑动，能近似刻画小虎所在位置距出发点O的距离S与时间t之间的函数关系的大致图象是（ ）
2．将二次函数y=x2的图象如何平移可得到y=x2-2x+2的图象（ ）
| A． | 向左平移2个单位，向上平移2个单位 | |
| B． | 向右平移2个单位，向下平移2个单位 | |
| C． | 向右平移1个单位，向上平移1个单位 | |
| D． | 向左平移1个单位，向下平移1个单位 |