题目内容
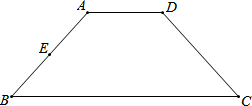 已知等腰梯形ABCD中,AD∥BC,AD=2,AB=3,BC=6,点E为边AB中点,点F是边BC上一动点,线段CE与线段DF交于点G,连接AG,若△ADG∽△DFC时,则线段CF的长为
已知等腰梯形ABCD中,AD∥BC,AD=2,AB=3,BC=6,点E为边AB中点,点F是边BC上一动点,线段CE与线段DF交于点G,连接AG,若△ADG∽△DFC时,则线段CF的长为考点:等腰梯形的性质,相似三角形的判定与性质
专题:
分析:根据两三角形相似,对应线段的比相等,求出线段CF的长.
解答:
解:∵ABCD是等腰梯形,AD=2,BC=6,
∵AD∥BC,
∴∠ADG=∠DFC,
∵△ADG∽△CDF,
∴∠DAG=∠FDC.
延长AG交BC于点T,可得△ABT∽△FCD,
则
=
,由AD∥BC得
=
=
,
设BF=x,可得FT=
,
∴
=
,
整理得:3x2-12x=0,
解得:x=4,x=0
∴CF=2,或CF=BC=6.

解:∵ABCD是等腰梯形,AD=2,BC=6,
∵AD∥BC,
∴∠ADG=∠DFC,
∵△ADG∽△CDF,
∴∠DAG=∠FDC.
延长AG交BC于点T,可得△ABT∽△FCD,
则
| AB |
| BT |
| FC |
| CD |
| AD |
| FT |
| DG |
| GF |
| DM |
| CF |
设BF=x,可得FT=
| 6-x |
| 4 |
∴
| 3 | ||
x+
|
| 6-x |
| 3 |
整理得:3x2-12x=0,
解得:x=4,x=0
∴CF=2,或CF=BC=6.
点评:本题考查的是相似三角形的判定与性质以及等腰梯形的性质,根据两三角形相似,得出对应线段的比相等,求得答案.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
用10米长的铝材制成一个矩形窗框,使它的面积为6平方米.若设它的一条边长为x米,则根据题意可列出关于x的方程为( )
| A、x(5+x)=6 |
| B、x(5-x)=6 |
| C、x(10-x)=6 |
| D、x(10-2x)=6 |
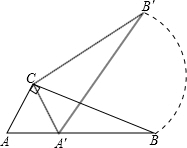 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( ) 如图,已知在平面直角坐标系xOy中,O是坐标原点,抛物线y=-x2+bx+c(c>0)的顶点为D,与y轴的交点为C,过点C作CA∥x轴交抛物线于点A,在AC延长线上取点B,使BC=
如图,已知在平面直角坐标系xOy中,O是坐标原点,抛物线y=-x2+bx+c(c>0)的顶点为D,与y轴的交点为C,过点C作CA∥x轴交抛物线于点A,在AC延长线上取点B,使BC=