题目内容
已知关于x的方程(k-1)x2-(k-1)x+
=0有两个相等的实数根,求k的值.
| 1 |
| 4 |
考点:根的判别式,一元二次方程的定义
专题:
分析:根据根的判别式令△=0,建立关于k的方程,解方程即可.
解答:解:∵关于x的方程(k-1)x2-(k-1)x+
=0有两个相等的实数根,
∴△=0,
∴[-(k-1)]2-4(k-1)×
=0,
整理得,k2-3k+2=0,
即(k-1)(k-2)=0,
解得:k=1(不符合一元二次方程定义,舍去)或k=2.
∴k=2.
| 1 |
| 4 |
∴△=0,
∴[-(k-1)]2-4(k-1)×
| 1 |
| 4 |
整理得,k2-3k+2=0,
即(k-1)(k-2)=0,
解得:k=1(不符合一元二次方程定义,舍去)或k=2.
∴k=2.
点评:本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
| A、平均数 | B、标准差 |
| C、中位数 | D、众数 |
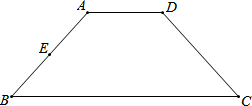 已知等腰梯形ABCD中,AD∥BC,AD=2,AB=3,BC=6,点E为边AB中点,点F是边BC上一动点,线段CE与线段DF交于点G,连接AG,若△ADG∽△DFC时,则线段CF的长为
已知等腰梯形ABCD中,AD∥BC,AD=2,AB=3,BC=6,点E为边AB中点,点F是边BC上一动点,线段CE与线段DF交于点G,连接AG,若△ADG∽△DFC时,则线段CF的长为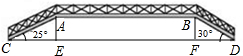 如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°
如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°