Question

如图，AD⊥CB于D，EF⊥CB于F，∠1=∠2，∠BAC=70°，求∠AGD的度数．

Answer 1

考点：平行线的判定与性质

专题：

分析：由EF∥AD，可得∠2=∠3，由等量代换可得∠1=∠3，可得DG∥BA，根据平行线的性质可得∠BAC+∠AGD=180°，即可求解．

解答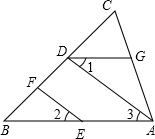：解：解：∵EF∥AD（已知），
∴∠2=∠3（两直线平行，同位角相等）；
∵∠1=∠2（已知），
∴∠1=∠3（等量代换）；
∴DG∥AB（内错角相等，两直线平行）．
∴∠BAC+∠AGD=180°（两直线平行，同旁内角互补）．
∵∠BAC=70°，
∴∠AGD=110°．

点评：此题考查了平行线的性质与判定，关键是掌握两直线平行，同位角相等，同旁内角互补．