题目内容
 如图,大半圆的弦AB平行于直径CD,且与小半圆相切,已知AB=16cm,求图中阴影部分的面积.
如图,大半圆的弦AB平行于直径CD,且与小半圆相切,已知AB=16cm,求图中阴影部分的面积.考点:切线的性质,勾股定理,垂径定理
专题:
分析:连接OB,作OE⊥AB于E,根据已知条件,根据勾股定理可将直角三角形的各边长表示出来,阴影的面积等于以OB和OE为半径的半圆的面积差.
解答: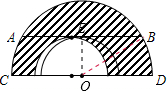 解:连接OB,作OE⊥AB于E,
解:连接OB,作OE⊥AB于E,
∵大半圆的弦AB平行于直径CD,
∴OE等于小圆的半径,
∵OE⊥AB,
∴EB=
AB=8,
在Rt△OBE中,
OB2=OE2+EB2,
∴OB2-OE2=EB2=64,
S阴影=
π-
π=
π=32πcm2.
 解:连接OB,作OE⊥AB于E,
解:连接OB,作OE⊥AB于E,∵大半圆的弦AB平行于直径CD,
∴OE等于小圆的半径,
∵OE⊥AB,
∴EB=
| 1 |
| 2 |
在Rt△OBE中,
OB2=OE2+EB2,
∴OB2-OE2=EB2=64,
S阴影=
| OB2 |
| 2 |
| OE2 |
| 2 |
| EB2 |
| 2 |
点评:此题考查了切线的性质,垂径定理以及勾股定理,遇到切线往往连接圆心与切点,构造直角三角形来解决问题.学生做题时注意:不规则图形面积的求法可用几个规则图形面积相加或相减求得.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
到三角形三边的距离都相等的点是三角形的( )
| A、三条角平分线的交点 |
| B、三条边的中线的交点 |
| C、三条高的交点 |
| D、三条边的垂直平分线的交点 |
某时装店同时卖出两件衣服,每件均卖168元,以成本计算,第一件盈利20%,另一件亏本20%,则本次出售中商场( )
| A、亏28元 | B、赚28元 |
| C、赚14元 | D、亏14元 |
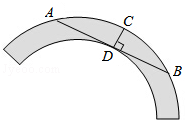 如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.
如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.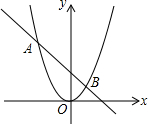 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx-c=0的解为
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx-c=0的解为