题目内容
5.已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E,如图1
(1)求证:AD•CD=BD•DE;
(2)若BD是边AC的中线,如图2,求$\frac{BD}{CE}$的值;
(3)如图3,连接AE.若AE=EC,求$\frac{BC}{CD}$的值.
分析 (1)直接判断出△ABD∽△ECD,即可得出结论;
(2)先设AB=AC=2a,CD=a,则BC=$\sqrt{2}$a,AD=a.求出BD,而△BAD∽△CED,得出$\frac{BD}{CD}=\frac{AB}{CE}$,代入求出CE即可解决问题.
(2)如图3,延长CE、BA相交于点F.只要证明△BEC≌△BEF,推出CE=EF,CF=2CE,由ABD≌△ACF,推出BD=CF,即可解决问题.
解答 解:(1)∵CE⊥BD,
∴∠A=∠E=90°,
∵∠ADB=∠EDC,
∴△BAD∽△CED,
∴$\frac{AD}{DE}=\frac{BD}{CD}$,
∴AD•CD=BD•DE;
(2)设CD=AD=a,则AB=AC=2a.
在Rt△ABD中,由勾股定理得:BD=$\sqrt{5}$a,
由(1)知,△BAD∽△CED,
∴$\frac{BD}{CD}=\frac{AB}{CE}$,
∴$\frac{\sqrt{5}a}{a}=\frac{2a}{CE}$,
解得:CE=$\frac{2\sqrt{5}}{5}$a,
∴$\frac{BD}{CE}$=$\frac{\sqrt{5}a}{\frac{2\sqrt{5}}{5}a}$=$\frac{5}{2}$;
(3)如图3,延长CE、BA相交于点F.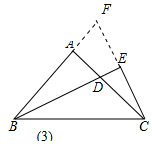
∵BE是∠ABC的角平分线,且BE⊥CF
在△BEC和△BEF中,$\left\{\begin{array}{l}{EF=CE}\\{∠BEF=∠BEC}\\{BE=BE}\end{array}\right.$,
∴△BEC≌△BEF,
∴CE=EF,
∴CF=2CE
又∵∠ABD+∠ADB=∠CDE+∠ACF=90°,
且∠ADB=∠CDE,
∴∠ABD=∠ACF
∵AB=AC,∠BAD=∠CAF=90°,
在△ABD和△ACF中,$\left\{\begin{array}{l}{∠ABD=∠ACF}\\{AB=AC}\\{∠BAD=∠CAF}\end{array}\right.$,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∴BD=2CE,
∴$\frac{BD}{CE}$=2.
点评 此题是相似形综合题,主要考查了相似三角形的判定和性质、全等三角形的判定和性质,等腰直角三角形的性质、三角形中线、角平分线的定义、勾股定理等知识,解题的关键是学会添加辅助线构造全等三角形解决问题,学会利用参数解决问题,属于中考常考题型.

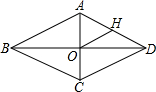 如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
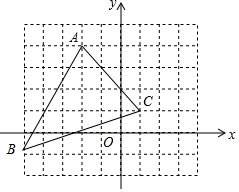 如图,若将△ABC先向右平移5个单位长度(1格代表1个单位长度),再向下平移3个单位长度得到△A1B1C1,则点A的对应点A1的坐标是( )
如图,若将△ABC先向右平移5个单位长度(1格代表1个单位长度),再向下平移3个单位长度得到△A1B1C1,则点A的对应点A1的坐标是( )| A. | (3,1) | B. | (9,-4) | C. | (-6,7) | D. | (-1,2) |
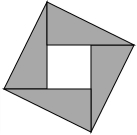 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )| A. | 25 | B. | 19 | C. | 13 | D. | 169 |
| A. | 2 | B. | 1 | C. | -2 | D. | 任意数 |
 如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AD∥BC.
如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AD∥BC. 如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.