题目内容
10.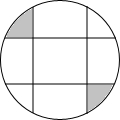 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )| A. | $\sqrt{2}$π | B. | 2-π | C. | π | D. | 2π |
分析 根据条件先确定小正方形面积与阴影部分面积的关系,再求出这个正方形的外接圆的面积与图中阴影部分面积的比值即可.
解答 解:如图 用a、b、c表示图中相应部分的面积.
用a、b、c表示图中相应部分的面积.
由题意:4(a+2b)=4a+4b+c,
∴c=4b,
∴小正方形的面积=阴影部分面积的2倍,
设小正方形的边长为x,则外接圆的面积=$\frac{π}{2}$x2,
∴这个正方形的外接圆的面积与图中阴影部分面积的比值=$\frac{π}{2}$x2:$\frac{1}{2}$x2=π.
故选C.
点评 本题考查正多边形与圆,圆的面积,正方形的外接圆面积与正方形面积的关系,解题的关键是用方程的思想解决问题,需要掌握正多边形与圆的位置关系.

练习册系列答案
相关题目
1.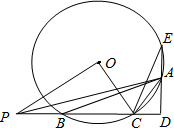 如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
(1)若∠ACB=120°,求证:CE=⊙O的半径.
(2)连OC,OP⊥OC交CB的延长线于P,若⊙O的半径为5cm,弦BC=6cm,求PB的长.
 如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E(1)若∠ACB=120°,求证:CE=⊙O的半径.
(2)连OC,OP⊥OC交CB的延长线于P,若⊙O的半径为5cm,弦BC=6cm,求PB的长.
5. 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:| 计算次数 | 计算结果 |
| 1 | -2 |
| 2 | 4 |
| 3 | 28 |
15. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )| A. | 8 | B. | 10 | C. | 2$\sqrt{21}$或8 | D. | 2$\sqrt{21}$或10 |
2.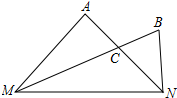 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )| A. | 若α=β,则点C在MN的垂直平分线上 | |
| B. | 若α+β=180°,则∠AMB=∠NMB | |
| C. | ∠MCN=$(\frac{α+β}{3}+60)$° | |
| D. | 当∠MCN=120°时,延长MA、NB交于点O,则OA=OB |
20.计算(-$\frac{1}{2}$x3y)2的结果是( )
| A. | $\frac{1}{2}$x4y2 | B. | -$\frac{1}{4}$x6y2 | C. | $\frac{1}{4}$x6y2 | D. | $\frac{1}{2}$x6y2 |
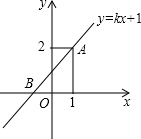 如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$). 浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?
浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?