题目内容
2.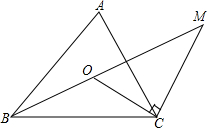 △ABC中,点O是∠ABC和∠ACB的平分线的交点.CM⊥OC,交BO延长线于点M.若∠A=70°,则∠M=( )°.
△ABC中,点O是∠ABC和∠ACB的平分线的交点.CM⊥OC,交BO延长线于点M.若∠A=70°,则∠M=( )°.| A. | 30 | B. | 35 | C. | 37.5 | D. | 40 |
分析 根据三角形的内角和求得∠ABC+∠ACB=180°-∠A=110°,根据点O是∠ABC和∠ACB的平分线的交点,于是得到∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=55°,由外角的性质得到∠MOC=55°,即可得到结论.
解答 解:∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°,
∵点O是∠ABC和∠ACB的平分线的交点,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=55°,
∴∠MOC=55°,
∵CM⊥OC,
∴∠M=35°.
故选B.
点评 本题考查了三角形的内角和,角平分线的性质,三角形外角的性质,熟记三角形的内角和是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.有6张写有数字的卡片,它们的背面都相同,现将它们背面朝上(如图所示),从中任意一张是数字1的概率是( )


| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
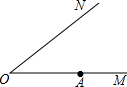 如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的?
如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的? 如图,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5cm,BE=10cm,BD=9cm,CD=5cm,求AF、FG、GD的长.
如图,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5cm,BE=10cm,BD=9cm,CD=5cm,求AF、FG、GD的长. 如图,已知∠AOB,画图并回答:
如图,已知∠AOB,画图并回答:



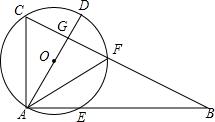 如图,在Rt△ABC中,∠BAC=90°,过A、C两点作⊙O交直角边AB于另一点E,交斜边BC于另一点F,直径AD交BC于点G.
如图,在Rt△ABC中,∠BAC=90°,过A、C两点作⊙O交直角边AB于另一点E,交斜边BC于另一点F,直径AD交BC于点G.