题目内容
1. 如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,
如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,(1)求供水站M到公路AB的垂直距离MD的长度.
(2)求小区A到供水站M的距离.(结果可保留根号)
分析 (1)根据题意,在△ABM中,∠BAM=30°,∠ABM=45°,BM=300($\sqrt{3}$+l)米.通过解直角Rt△MBD求得MD的长度;
(2)通过解直角Rt△ADM求得AM的长度.
解答 解:由题意可知∠MBD=45°,∠MAD=30°.
(1)在Rt△MBD中,DM=BM•sin∠DBM=300×sin45°=150$\sqrt{2}$(米);
(2)在Rt△ADM中,AM=$\frac{DM}{sin∠DAM}$=$\frac{150\sqrt{2}}{sin30°}$=300$\sqrt{2}$(米).
点评 本题考查了解直角三角形的应用--方向角问题.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.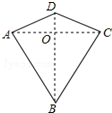 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )
 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
6.方程3x2-7x=0中,常数项是( )
| A. | 3 | B. | -7 | C. | 7 | D. | 0 |
10. 如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.
如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.
 如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.
如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.| A. | 8$\sqrt{6}$+24 | B. | 8$\sqrt{6}$+8 | C. | 24+8$\sqrt{3}$ | D. | 8+8$\sqrt{3}$ |

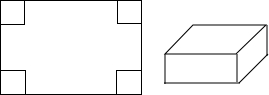 如图是以长为120cm,宽为80cm的长方形硬纸,在它的四个角处各剪去一个边长为20cm的正方形后,将其折叠成如图所示的无盖的长方体,则这个长方体的体积为64000立方厘米.
如图是以长为120cm,宽为80cm的长方形硬纸,在它的四个角处各剪去一个边长为20cm的正方形后,将其折叠成如图所示的无盖的长方体,则这个长方体的体积为64000立方厘米.