题目内容
19.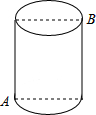 如图,一圆柱高8cm,底面圆周长为12cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是10cm.
如图,一圆柱高8cm,底面圆周长为12cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是10cm.
分析 先把圆柱的侧面展开,连接AB,利用勾股定理求出AB的长即可.
解答  解:如图所示:
解:如图所示:
连接AB,
∵圆柱高8cm,底面圆周长为12cm,
∴AC=$\frac{1}{2}$×12=6cm,
在Rt△ABC中,
AB=$\sqrt{A{C}^{2}+B{C}^{2}}=\sqrt{{6}^{2}+{8}^{2}}$=10cm.
故答案为:10
点评 本题考查的是平面展开-最短路径问题,解答此类问题的关键是画出圆柱的侧面展开图,利用勾股定理进行解答.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.函数y=m${x}^{{m}^{2}-3}$+2-m是正比例函数,则m的值为( )
| A. | m不为0 | B. | m=2 | C. | m=-2 | D. | m=2或-2 |
11.已知a2+Nab+64b2是一个完全平方式,则N等于( )
| A. | 8 | B. | ±8 | C. | ±16 | D. | ±32 |
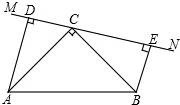 在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且
在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且