题目内容
13.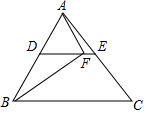 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=16,BC=18,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=16,BC=18,则EF的长为1.
分析 先根据三角形中位线定理求出DE的长,再由直角三角形的性质得出DF的长,根据EF=DE-DF即可得出结论.
解答 解:∵DE为△ABC的中位线,BC=18,
∴DE=$\frac{1}{2}$BC=9.
∵∠AFB=90°,AB=16,
∴DF=$\frac{1}{2}$AB=8,
∴EF=DE-DF=9-8=1.
故答案为:1.
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
3.计算tan60°的值等于( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
8.若2m-5与4m-9是某一个正数的平方根,则m的值是( )
| A. | $\frac{7}{3}$ | B. | -1 | C. | $\frac{7}{3}$或2 | D. | 2 |
3.已知直角三角形的一直角边长为$\sqrt{5}$,斜边上的高为2,则这个直角的斜边长为( )
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{5\sqrt{2}}{2}$ |
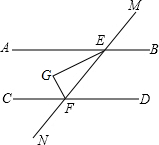 如图,AB∥CD,直线MN分别交AB、CD于点E,F,EG平分∠AEF,EG⊥FG于点G,若∠BEM=60°,则∠CFG=60°.
如图,AB∥CD,直线MN分别交AB、CD于点E,F,EG平分∠AEF,EG⊥FG于点G,若∠BEM=60°,则∠CFG=60°.