题目内容
8.若2m-5与4m-9是某一个正数的平方根,则m的值是( )| A. | $\frac{7}{3}$ | B. | -1 | C. | $\frac{7}{3}$或2 | D. | 2 |
分析 依据平方根的性质列出关于m的方程,可求得m的值.
解答 解:∵2m-5与4m-9是某一个正数的平方根,
∴2m-5=4m-9或2m-5+4m-9=0.
解得:m=2或m=$\frac{7}{3}$.
故选:C.
点评 本题主要考查的是平方根的性质,熟练掌握平方根的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )
如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )
 如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )
如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )| A. | 70° | B. | 100° | C. | 110° | D. | 120° |
16.下列计算中,正确的是( )
| A. | $\root{3}{8}$=±2 | B. | $\root{6}{(-2)^{6}}$=$\root{3}{(-2)^{3}}$=-2 | C. | -$\sqrt{(-2)^{2}}$=2 | D. | ($\frac{1}{64}$)${\;}^{\frac{1}{6}}$=$\frac{1}{2}$ |
3.顺次连结四边形四条边的中点,所得的四边形是矩形,则原四边形一定是( )
| A. | 平行四边形 | B. | 对角线相等的四边形 | ||
| C. | 对角线互相垂直的四边形 | D. | 矩形 |
17.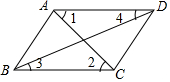 如图,下列条件中不能判定AD∥BC的是( )
如图,下列条件中不能判定AD∥BC的是( )
 如图,下列条件中不能判定AD∥BC的是( )
如图,下列条件中不能判定AD∥BC的是( )| A. | ∠BAD+∠ABC=180° | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠BAD=∠BCD |
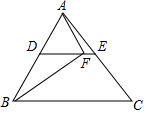 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=16,BC=18,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=16,BC=18,则EF的长为1.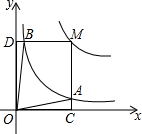 反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.
反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.