题目内容
18.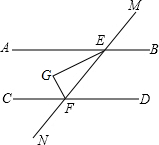 如图,AB∥CD,直线MN分别交AB、CD于点E,F,EG平分∠AEF,EG⊥FG于点G,若∠BEM=60°,则∠CFG=60°.
如图,AB∥CD,直线MN分别交AB、CD于点E,F,EG平分∠AEF,EG⊥FG于点G,若∠BEM=60°,则∠CFG=60°.
分析 首先由AB∥CD,根据两直线平行,同旁内角互补,即可求得∠CFE的度数,又由内角和定理,求得∠GFE的度数,则可求得∠CFG的度数.
解答 解:∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵∠AEF=∠BEM=60°,
∴∠CFE=120°,
∵EG平分∠AEF,
∴∠GEF=$\frac{1}{2}$∠AEF=30°,
∵EG⊥FG,
∴∠EGF=90°,
∴∠GFE=90°-∠GEF=60°,
∴∠CFG=∠CEF-∠GFE=60°.
故答案为:60°.
点评 此题考查了平行线的性质,垂直的定义以及角平分线的性质.注意两直线平行,同旁内角互补.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
8. 如图是一个由5个相同正方体组成的立体图形,它的俯视图是( )
如图是一个由5个相同正方体组成的立体图形,它的俯视图是( )
 如图是一个由5个相同正方体组成的立体图形,它的俯视图是( )
如图是一个由5个相同正方体组成的立体图形,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
9.在平行四边形ABCD中,对角线AC、BD相交于点O,下列式子中一定成立的是( )
| A. | AC⊥BD | B. | OA=OC | C. | AC=BD | D. | OA=OD |
8.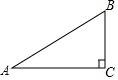 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{4}{5}$ |
 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=1.
如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=1.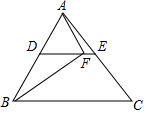 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=16,BC=18,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=16,BC=18,则EF的长为1.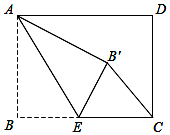 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,CB′的长为2或$\sqrt{10}$.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,CB′的长为2或$\sqrt{10}$.