题目内容
3.已知直角三角形的一直角边长为$\sqrt{5}$,斜边上的高为2,则这个直角的斜边长为( )| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{5\sqrt{2}}{2}$ |
分析 可设另一条直角边为x,根据勾股定理得到斜边长$\sqrt{5+{x}^{2}}$,再根据三角形面积公式得到关于x的方程,解方程可求另一条直角边,进一步得到斜边长.
解答 解:设另一条直角边为x,则斜边长$\sqrt{5+{x}^{2}}$,依题意有
$\sqrt{5}$x÷2=2$\sqrt{5+{x}^{2}}$÷2,
解得x1=-2$\sqrt{5}$,x2=2$\sqrt{5}$,
$\sqrt{5+{x}^{2}}$=$\sqrt{5+20}$=5.
则这个直角的斜边长为5.
故选:C.
点评 本题考查了利用勾股定理求直角三角形的边长及利用面积法求直角三角形的高,是解此类题目常用的方法.

练习册系列答案
相关题目
11.已知x≠0且M=(x2+2x+1)(x2-2x+1),N=(x2+x+1)(x2-x+1),则M与N的大小关系为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
8.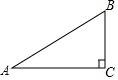 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{4}{5}$ |
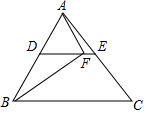 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=16,BC=18,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=16,BC=18,则EF的长为1.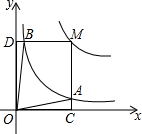 反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.
反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.
 如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.