题目内容
2.在平面直角坐标系内,点P(x-2,x+1)在第二象限,则x的取值范围是-1<x<2.分析 根据题意,点P(x-2,x+1)在第二象限判断出该点的横纵坐标的符号,进而判断x的取值范围.
解答 解:根据平面直角坐标系性质,
第二象限横坐标为负纵坐标为正,
即:x-2<0,x+1>0,
∴-1<x<2,
故答案为-1<x<2.
点评 解决本题的关键是掌握好平面直角坐标系中四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
5.若分式$\frac{2}{x-2}$无意义,则x的值为( )
| A. | x=-1 | B. | x=1 | C. | x=1 | D. | x=2 |
10. 将一副直角三角尺如图放置,已知AE∥BC,则∠EFC的度数是( )
将一副直角三角尺如图放置,已知AE∥BC,则∠EFC的度数是( )
 将一副直角三角尺如图放置,已知AE∥BC,则∠EFC的度数是( )
将一副直角三角尺如图放置,已知AE∥BC,则∠EFC的度数是( )| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
12.已知菱形ABCD的对角线AC,BD的长度是关于x的方程x2-14x+48=0的两个实数根,则此菱形的面积是( )
| A. | 20 | B. | 24 | C. | 48 | D. | 不确定 |
 如图,DE是△ABC的中位线,△ADE的面积为3cm2,则△ABC的面积为12 cm2.
如图,DE是△ABC的中位线,△ADE的面积为3cm2,则△ABC的面积为12 cm2.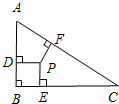 如图,△ABC中,∠B=90°,两直角边AB=3,BC=4,AC=5.三角形内有一点P到各边的距离相等,则这个距离为( )
如图,△ABC中,∠B=90°,两直角边AB=3,BC=4,AC=5.三角形内有一点P到各边的距离相等,则这个距离为( )