题目内容
16.如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形.这一过程所揭示的乘法公式是(a+b)(a-b)=a2-b2.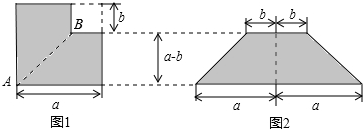
分析 先根据大正方形的面积减去小正方形的面积=梯形的面积,直接可写出乘法公式(a+b)(a-b)=a2-b2.
解答 解:∵大正方形的边长为a,小正方形的边长为b,
∴阴影部分的面积=a2-b2.
∵梯形的面积=$\frac{1}{2}(2a+2b)(a-b)$=(a+b)(a-b),
∴(a+b)(a-b)=a2-b2.
故答案为:(a+b)(a-b)=a2-b2.
点评 本题考查了平方差公式,解决本题的关键是熟记平方差公式.

练习册系列答案
相关题目
11.下列说法中正确的是:所有的( )都相似.
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
6.计算25m÷5m的结果为( )
| A. | 5 | B. | 5m | C. | 20 | D. | 20m |
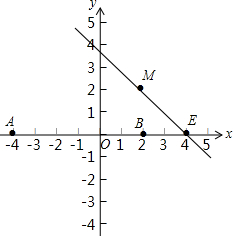 如图,x轴上两个点A(-4,0),B(2,0),直线l经过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
如图,x轴上两个点A(-4,0),B(2,0),直线l经过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.