题目内容
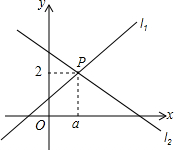 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2).(1)求a的值;
(2)不解关于x,y的方程组
|
(3)请直接写出关于x的不等式x+1≥mx+n的解集.
考点:一次函数与二元一次方程(组),一次函数与一元一次不等式
专题:数形结合
分析:(1)根据一次函数图象上点的坐标特征,把把P(a,2)代入y=x+1即可求出a的值;
(2)由(1)得到P点坐标(1,2),根据一次函数与二元一次方程组的关系即可得到方程组的解;
(3)观察函数图象得到当x≥1时,直线l1:y=x+1都在直线l2:y=mx+n的上方(含交点P).
(2)由(1)得到P点坐标(1,2),根据一次函数与二元一次方程组的关系即可得到方程组的解;
(3)观察函数图象得到当x≥1时,直线l1:y=x+1都在直线l2:y=mx+n的上方(含交点P).
解答:解:(1)把P(a,2)代入y=x+1得a+1=2,解得a=1;
(2)由(1)得P点坐标为(1,2),
所以程组
的解为
;
(3)关于x的不等式x+1≥mx+n的解集是x≥1.
(2)由(1)得P点坐标为(1,2),
所以程组
|
|
(3)关于x的不等式x+1≥mx+n的解集是x≥1.
点评:本题考查了一次函数与二元一次方程(组):两个一次函数的交点坐标是有两个函数解析式所组成的方程组的解.也考查了一次函数与一元一次不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数:y=x(8-x),y=1-
x2,y=
,y=x2-
,其中以x为自变量的二次函数有( )
| 1 |
| 2 |
| x2-4 |
| 6 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知三点P1(x1,y1),P2(x2,y2),P3(x3,y3)都在反比例函数y=-
的图象上,且x1<0<x2<x3,则下列式子正确的是( )
| 2 |
| x |
| A、y1>y2>y3 |
| B、y1>y3>y2 |
| C、y2>y3>y1 |
| D、y3>y2>y1 |
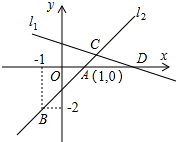 如图,直线l1的解析表达式为y=-
如图,直线l1的解析表达式为y=- 画图题:如图是单位长度是1的网格.
画图题:如图是单位长度是1的网格.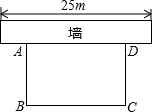 如图所示:某居民小区要在一块要边靠墙(墙长25m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边由总长为40m的栅栏围成.
如图所示:某居民小区要在一块要边靠墙(墙长25m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边由总长为40m的栅栏围成.