题目内容
1.先化简,再求值:$\frac{x-4}{x-3}$÷(x+3-$\frac{7}{x-3}$),其中x=3.分析 先化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:$\frac{x-4}{x-3}$÷(x+3-$\frac{7}{x-3}$)
=$\frac{x-4}{x-3}÷\frac{(x+3)(x-3)-7}{x-3}$
=$\frac{x-4}{x-3}×\frac{x-3}{(x+4)(x-4)}$
=$\frac{1}{x+4}$,
当x=3时,原式=$\frac{1}{3+4}=\frac{1}{7}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
12.方程x2-8x+17=0的根的情况是( )
| A. | 两实数根的和为-8 | B. | 两实数根的积为17 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
6.下列汽车标志不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
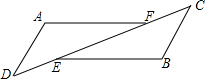 如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.
如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF. 如图,在Rt△ABC中,∠C=90°,tanA=$\frac{3}{4}$,BC=12,求AB的长.
如图,在Rt△ABC中,∠C=90°,tanA=$\frac{3}{4}$,BC=12,求AB的长. 如图,点A、B在数轴上表示的实数分别是-2和10,点C是线段AB上的一点且AC=3BC,求点C表示的数.
如图,点A、B在数轴上表示的实数分别是-2和10,点C是线段AB上的一点且AC=3BC,求点C表示的数. 如图,在同一时刻,测得小丽和旗杆的影长分别为1m和6m,小华的身高约为1.8m,则旗杆的高约为10.4m.
如图,在同一时刻,测得小丽和旗杆的影长分别为1m和6m,小华的身高约为1.8m,则旗杆的高约为10.4m.