题目内容
14.先化简,再求值:$\frac{{{x^2}-4}}{{{x^2}-4x+4}}$÷$\frac{x+2}{x+1}$-$\frac{x}{x-2}$,其中x=2+$\sqrt{2}$.分析 根据分式的混合运算法则把原式化简,代入计算即可.
解答 解:$\frac{{{x^2}-4}}{{{x^2}-4x+4}}$÷$\frac{x+2}{x+1}$-$\frac{x}{x-2}$
=$\frac{(x+2)(x-2)}{(x-2)^{2}}$×$\frac{x+1}{x+2}$-$\frac{x}{x-2}$
=$\frac{x+1}{x-2}$-$\frac{x}{x-2}$
=$\frac{1}{x-2}$,
当x=2+$\sqrt{2}$时,原式=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,掌握分式的混合运算法则是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:标准分=个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学、英语哪个学科考得更好?
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | $\sqrt{2}$ | |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式:标准分=个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学、英语哪个学科考得更好?
4.已知点M(3,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为( )
| A. | 相交,相交 | B. | 平行,平行 | C. | 垂直相交,平行 | D. | 平行,垂直相交 |
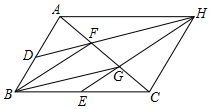 已知:如图,在△ABC中,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H.
已知:如图,在△ABC中,点D、E分别是边AB、BC的中点,点F、G是边AC的三等分点,DF、EG的延长线相交于点H.