题目内容
17.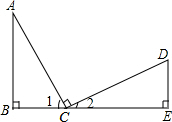 已知:如图所示,B、C、E三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,B、C、E三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A与∠D互为余角 | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | ∠1=60°,∠2=30° |
分析 先利用互余得到∠1+∠A=90°,∠2+∠D=90°,∠1+∠2=90°,则根据等角的余角相等得到∠A=∠2,∠1=∠D,且∠A+∠D=90°,然后根据“ASA”可判定△ABC≌△CED,从而可对各选项进行判定.
解答 解:∵∠B=∠E=90°,
∴∠1+∠A=90°,∠2+∠D=90°,
∵AC⊥CD,
∴∠1+∠2=90°,
∴∠A=∠2,∠1=∠D,∠A+∠D=90°,
在△ABC和△CED中
$\left\{\begin{array}{l}{∠A=∠2}\\{AC=CD}\\{∠1=∠D}\end{array}\right.$,
∴△ABC≌△CED.
故选D.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列四组变形中,变形正确的是( )
| A. | 由5x+7=0,得5x=-7 | B. | 由2x-3=0,得2x-3+3=0 | ||
| C. | 由$\frac{x}{4}$=2,得x=$\frac{1}{2}$ | D. | 由3x=5,得x=15 |
8.菱形的两条对角线长分别为9cm和4cm,则此菱形的面积是( )
| A. | 16cm2 | B. | 4$\sqrt{13}$cm2 | C. | 18cm2 | D. | 2$\sqrt{13}$cm2 |
5.下列计算正确的是( )
| A. | 23=6 | B. | -32=9 | C. | (-1)2=1 | D. | 2÷6×$\frac{1}{3}$=1 |
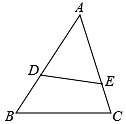 如图,△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,若四边形BCED的面积是10,则△ADE的面积是8.
如图,△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,若四边形BCED的面积是10,则△ADE的面积是8.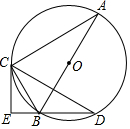 如图,AB为⊙O直径,C、D为⊙O上的点,CE⊥DB交DB的延长线于点E,且∠CBE=∠ABC.
如图,AB为⊙O直径,C、D为⊙O上的点,CE⊥DB交DB的延长线于点E,且∠CBE=∠ABC.