题目内容
2.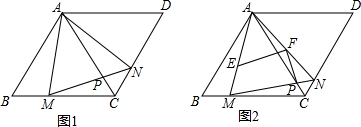 如图1,在边长为4的菱形ABCD中,AC为其对角线,∠ABC=60°点M、N分别是边BC、边CD上的动点,且MB=NC.连接AM、AN、MN.MN交AC于点P.
如图1,在边长为4的菱形ABCD中,AC为其对角线,∠ABC=60°点M、N分别是边BC、边CD上的动点,且MB=NC.连接AM、AN、MN.MN交AC于点P.(1)△AMN是什么特殊的三角形?说明理由.并求其面积最小值;
(2)求点P到直线CD距离的最大值;
(3)如图2,已知MB=NC=1,点E、F分别是边AM、边AN上的动点,连接EF、PF,EF+PF是否存在最小值?若存在,求出最小值及此时AE、AF的长;若不存在,请说明理由.
分析 (1)△AMN是等边三角形,AM⊥BC时面积最小.只要证明△AMB≌△ANC,推出AM=AN,∠BAM=∠CAN即可解决问题.
(2)如图2中,当AM⊥BC时,点P到CD距离最大.作PE⊥CD于E.
(3)如图3中,作点P关于AN的对称点为K,过点K做AM的垂线,交AN为F,交AM为E,此时,EF+PF最短,连接AK、作AG⊥MN于G,MH⊥AB于H.首先求出AM、AG的长,再证明△AGP≌△KEA,推出KE=AG即可.
解答 解:(1)如图1中,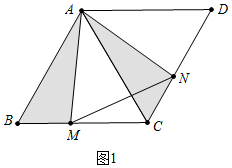
∵ABCD是菱形,∠ABC=60°,
∴△ABC为等边三角形
在△AMB和△ANC中,
AB=AC
∠B=∠ACN=60°
BM=NC
∴△AMB≌△ANC
∴AM=AN,∠BAM+∠MAC=∠MAC+∠NAC=60°,
∴∠MAN=60°,
∴△AMN为等边三角形,
当AM⊥BC时,△AMN的边长最小,面积最小,
此时AM=MN=AN=2$\sqrt{3}$,S△AMN=$\frac{\sqrt{3}}{4}$•(2$\sqrt{3}$)2=3$\sqrt{3}$
(2)如图2中,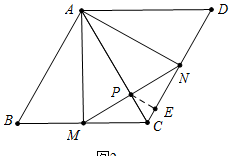
当AM⊥BC时,点P到CD距离最大.作PE⊥CD于E.
理由:由(1)可知△AMN是等边三角形,
当AM⊥BC时,△AMN的边长最小,此时PA长最小,PC的长最大,点P到直线CD距离的最大,
∵BM=MC=2,∠CMP=30°,∠MPC=90°,
∴PC=$\frac{1}{2}$MC=1,
在Rt△PCE中,∵∠CPE=30°,PC=1,
∴EC=$\frac{1}{2}$PC=$\frac{1}{2}$,
∴PE=$\sqrt{P{C}^{2}-C{E}^{2}}$=$\frac{\sqrt{3}}{2}$.
∴点P到直线CD距离的最大值为$\frac{\sqrt{3}}{2}$;
(3)如图3中,作点P关于AN的对称点为K,过点K做AM的垂线,交AN为F,交AM为E,此时,EF+PF最短,由于对称,PF=KF,EF为垂线段(垂线段最短).
连接AK、作AG⊥MN于G,MH⊥AB于H.
在Rt△BMH中,∵BM=1,∠BMH=30°,
∴BH=$\frac{1}{2}$,HM=$\frac{\sqrt{3}}{2}$,
∴AH=$\frac{7}{2}$,AM=$\sqrt{A{H}^{2}+H{M}^{2}}$=$\sqrt{13}$,
∵△AMN是等边三角形,
∴AG=$\frac{\sqrt{39}}{2}$.
∵∠APG=∠PCM+∠PMC=60°+∠PMC,
∵∠PMC+∠PCM+∠CPM=180°,∠NAP+∠ANP+∠APN=180°,∠ANP=∠PCM=60°,∠APN=∠CPM,
∴∠CMP=∠NAP=∠NAK,
∵∠EAK=∠EAN+∠NAK=60°+∠NAK,
∴∠APG=∠EAK,
∵∠AGP=∠AEK=90°,AP=AK,
∴△AGP≌△KEA,
∴KE=AG=$\frac{\sqrt{39}}{2}$.
∴EF+PF的最小值为$\frac{\sqrt{39}}{2}$,
∵∠PCN=∠PCM,
∴$\frac{{S}_{△PCN}}{{S}_{△PCM}}$=$\frac{PN}{PM}$=$\frac{\frac{1}{2}•CN•h}{\frac{1}{2}•CM•h}$=$\frac{CN}{CM}$=$\frac{1}{3}$,
∴PN=$\frac{\sqrt{13}}{4}$,
∴AE=PG=GN-PN=$\frac{\sqrt{13}}{4}$,
∵在Rt△AFE中,∠AFE=30°,∴AF=2AE,
∴AF=$\frac{\sqrt{13}}{2}$.
点评 本题考查四边形综合题、菱形的性质、等边三角形的性质、全等三角形的判定和性质、垂线段最短等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 如图,在△ABC中,∠A=75°,直线DE分别与边AB,AC交于D,E两点,则∠1+∠2=255°.
如图,在△ABC中,∠A=75°,直线DE分别与边AB,AC交于D,E两点,则∠1+∠2=255°.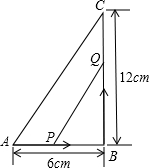 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发.
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发.