题目内容
12.已知tanα=$\frac{2}{5}$,α是锐角,求tan(9O°-α),sinα,cosα的值.分析 根据题意表示出AC,BC,AB的长,再利用锐角三角函数定义得出即可.
解答  解:∵如图所示:tanB=tanα=$\frac{2}{5}$,
解:∵如图所示:tanB=tanα=$\frac{2}{5}$,
∴设AC=2x,BC=5x,则AB=$\sqrt{29}$x,
∴tan(9O°-α)=$\frac{5x}{2x}$=$\frac{5}{2}$,
sinα=$\frac{AC}{AB}$=$\frac{2x}{\sqrt{29}x}$=$\frac{2\sqrt{29}}{29}$,
cosα=$\frac{BC}{AB}$=$\frac{5x}{\sqrt{29}x}$=$\frac{5\sqrt{29}}{29}$.
点评 此题主要考查了锐角三角函数定义,正确记忆锐角三角函数关系是解题关键.

练习册系列答案
相关题目
7.某市2010年平均房价为每平方米4000元.连续两年增长后,2012年平均房价达到每平方米5500元.设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
| A. | 5500(1+x)2=4000 | B. | 5500(1-x)2=4000 | C. | 4000(1-x)2=5500 | D. | 4000(1+x)2=5500 |
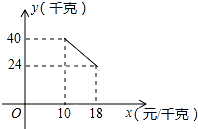 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: 二次函数y=ax2+bx+c的图象如图所示,则b2-4ac>0(填“>”“<”或“=”)
二次函数y=ax2+bx+c的图象如图所示,则b2-4ac>0(填“>”“<”或“=”)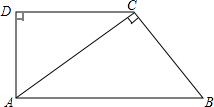 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm, 已知△ABC和一点O,以点O为位似中心,作△DEF,使它与△ABC位似,且相似比是2:1.
已知△ABC和一点O,以点O为位似中心,作△DEF,使它与△ABC位似,且相似比是2:1.