题目内容
13. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a<0;②b>0;③c>0;④b2-4ac>0,
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 |
分析 由开口方向可判断①,由对称轴可判断②,由与y轴的交点可判断③,由图象与x轴的交点个数可判断④,则可求得答案.
解答 解:
∵抛物线开口向上,
∴a>0,故①不正确;
∵对称轴为x=1,
∴-$\frac{b}{2a}$>0,且a>0,
∴b<0,故②不正确;
∵抛物线与y轴的交点在x轴的下方,
∴c<0,故③不正确;
∵抛物线与x轴有两个交点,
∴方向ax2+bx+c=0有两个不相等的实数根,
∴b2-4ac>0,故④正确;
综上可知正确的只有1个,
故选A.
点评 本题考查二次函数图象与系数的关系,二次函数的性质等知识,解题的关键是熟练运用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
5.下列各曲线中,不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
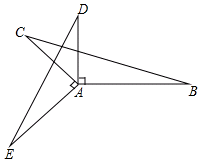 已知:∠EAC=∠DAB=90°,AB=AE,AC=AD,求证:△EAD≌△BAC.
已知:∠EAC=∠DAB=90°,AB=AE,AC=AD,求证:△EAD≌△BAC. 把棱长为1cm的若干个小正方体摆放成如图所示的几何体.
把棱长为1cm的若干个小正方体摆放成如图所示的几何体.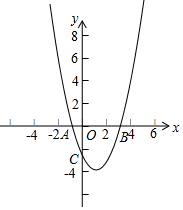 在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C(如图),点C的坐标为(0,-3),且BO=CO.
在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C(如图),点C的坐标为(0,-3),且BO=CO. 矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10,
矩形ABCD中,对角线AC和BD相交于O,∠AOB=60°,AC=10,