题目内容
3.解方程:(1)(x+1)2-4=0;
(2)12(2-x)2-9=0;
(3)x(3x+2)-6(3x+2)=0
(4)(x+2)2-16=0;
(5)(2x+3)2-25=0;
(6)4(1-3x)2=1.
分析 (1)先变形得到(x+1)2=4,然后利用直接开平方法解方程;
(2)先变形得到(2-x)2=$\frac{3}{4}$,然后利用直接开平方法解方程;
(3)利用因式分解法解方程;
(4)先变形得到(x+2)2=16,然后利用直接开平方法解方程;
(5)先变形得到(2x+3)2=25,然后利用直接开平方法解方程;
(6)先变形得(1-3x)2=$\frac{1}{4}$,然后利用直接开平方法解方程.
解答 解:(1)(x+1)2=4,
x+1=±2,
所以x1=1,x2=-3;
(2)(2-x)2=$\frac{3}{4}$
2-x=±$\frac{\sqrt{3}}{2}$,
所以x1=2-$\frac{\sqrt{3}}{2}$,x2=2+$\frac{\sqrt{3}}{2}$;
(3)x(3x+2)-6(3x+2)=0,
(3x+2)(x-6)=0,
3x+2=0或x-6=0,
所以x1=-$\frac{2}{3}$,x2=6;
(4)(x+2)2=16
x+2=±4,
所以x1=,2,x2=-6;
(5)(2x+3)2=25
2x+3=±5,
所以x1=1,x2=-4;
(6)(1-3x)2=$\frac{1}{4}$,
1-3x=±$\frac{1}{2}$,
所以x1=$\frac{1}{2}$,x2=-$\frac{1}{6}$.
点评 本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.也考查了因式分解法解方程.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
8.若1<x<2,则$\sqrt{{(x-3)}^{2}}$+$\sqrt{{(x-1)}^{2}}$的值为( )
| A. | 2x-4 | B. | -2 | C. | 4-2x | D. | 2 |
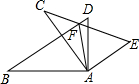 已知,如图,AB⊥AD,AC⊥AE,AB=AC,AD=AE.求证:
已知,如图,AB⊥AD,AC⊥AE,AB=AC,AD=AE.求证: 已知AD是BC边上的中线,AF=2FD,求证:AE=EC.
已知AD是BC边上的中线,AF=2FD,求证:AE=EC. 如图,
如图,