题目内容
13.计算:(1)($\frac{2x}{x-3}$-$\frac{x}{x+3}$)•$\frac{{x}^{2}-9}{x}$
(2)$\frac{{a}^{2}}{a-1}$-a-1
(3)解方程:$\frac{x-2}{x+2}$-1=$\frac{16}{{x}^{2}-4}$.
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,约分即可得到结果;
(2)原式通分并利用同分母分式的减法法则计算即可得到结果;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{2{x}^{2}+6x-{x}^{2}+3x}{(x+3)(x-3)}$•$\frac{(x+3)(x-3)}{x}$=x+9;
(2)原式=$\frac{{a}^{2}-(a+1)(a-1)}{a-1}$=$\frac{{a}^{2}-{a}^{2}+1}{a-1}$=$\frac{1}{a-1}$;
(3)去分母得:(x-2)2-x2+4=16,
解得:x=-2,
经检验x=-2是增根,分式方程无解.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.9的平方根是( )
| A. | 3 | B. | ±3 | C. | ±$\sqrt{3}$ | D. | ±81 |
 已知:一次函数y=2x-4
已知:一次函数y=2x-4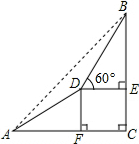 某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)