题目内容
12. 如图,
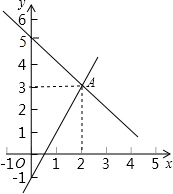
如图,(1)点A的坐标可以看成是方程组$\left\{\begin{array}{l}{y=-x+5}\\{y=2x-1}\end{array}\right.$ 的解.(写出解答过程)
(2)求出两直线与y轴所围成的三角形的面积.
分析 (1)先利用待定系数法分别求出两直线的解析式,然后根据函数图象交点坐标为两函数解析式组成的方程组的解即可得到答案;
(2)根据函数图象与坐标轴的交点坐标和两函数的交点坐标利用三角形的面积公式进行计算即可.
解答 解:(1)设过点(0,5)和点(2,3)的解析式为y=kx+b,
则$\left\{\begin{array}{l}{b=5}\\{2k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
所以该一次函数解析式为y=-x+5;
设过点(0,-1)和点(2,3)的解析式为y=mx+n,
则$\left\{\begin{array}{l}{n=-1}\\{2m+n=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=2}\\{n=-1}\end{array}\right.$,
所以该一次函数解析式为y=2x-1,
所以点A的坐标可以看成是方程组$\left\{\begin{array}{l}{y=-x+5}\\{y=2x-1}\end{array}\right.$解.
故答案为:$\left\{\begin{array}{l}{y=-x+5}\\{y=2x-1}\end{array}\right.$;
(2)围成的三角形的面积为:S=$\frac{1}{2}$[5-(-1)]×2=6.
点评 本题考查了一次函数与二元一次方程(组)的知识,函数图象交点坐标为两函数解析式组成的方程组的解.也考查了待定系数法求次函数解析式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 已知:一次函数y=2x-4
已知:一次函数y=2x-4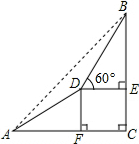 某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
某校数学兴趣小组为测量山高,在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进200米到达D处,在D处测得山顶B的仰角为60°,如图所示,求山的高度BC.(结果精确到1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)