题目内容
19.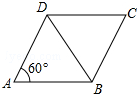 如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )
如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 连结AC交BD于O,如图,根据菱形的性质得AC⊥BD,OA=OC,AD=AB=2,则可判断△ADB为等边三角形,根据等边三角形的性质得OA=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$,所以AC=2OA=2$\sqrt{3}$.
解答 解:连结AC交BD于O,如图,
∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC,AD=AB=2,
而∠DAB=60°,
∴△ADB为等边三角形,
∴OA=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$,
∴AC=2OA=2$\sqrt{3}$.
故选D.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了等边三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.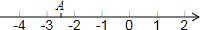 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )
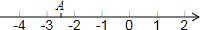 如图,在数轴上点A表示的数可能是( )
如图,在数轴上点A表示的数可能是( )| A. | -$\sqrt{2}$ | B. | -$\sqrt{8}$ | C. | -$\sqrt{5}$ | D. | -$\sqrt{10}$ |
8. 将一副三角板按如图所示方式放置,则∠1与∠2的和是( )
将一副三角板按如图所示方式放置,则∠1与∠2的和是( )
 将一副三角板按如图所示方式放置,则∠1与∠2的和是( )
将一副三角板按如图所示方式放置,则∠1与∠2的和是( )| A. | 60° | B. | 45° | C. | 30° | D. | 25° |
 已知a、b、c在数轴上的位置如图所示,试求|a+b|-|c-3|+|b-c|的值.
已知a、b、c在数轴上的位置如图所示,试求|a+b|-|c-3|+|b-c|的值. 关于x的不等式x-3>$\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是-12.
关于x的不等式x-3>$\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是-12.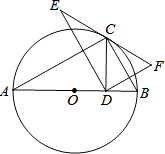 如图,点C在以AB为直径的⊙O上,∠CAB=30°,点D在AB上由点B开始向点A运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.
如图,点C在以AB为直径的⊙O上,∠CAB=30°,点D在AB上由点B开始向点A运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.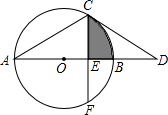 如图,AB为⊙O的直径,点C在⊙O上,过点C作CD交AB的延长线于点D,已知∠D=30°,弦CF⊥AB,垂足为E,且AC=2CE.
如图,AB为⊙O的直径,点C在⊙O上,过点C作CD交AB的延长线于点D,已知∠D=30°,弦CF⊥AB,垂足为E,且AC=2CE. 如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象.两地间的距离是80千米.请你根据图象回答或解决下面的问题:
如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象.两地间的距离是80千米.请你根据图象回答或解决下面的问题: 如图,∠A0B=60°,点P在0A上,点M、N在OB上,PM=PN,若OP=10,OM=4,则MN的长为( )
如图,∠A0B=60°,点P在0A上,点M、N在OB上,PM=PN,若OP=10,OM=4,则MN的长为( )