题目内容
4.在Rt△ABC中,∠C=90°,若tanA=20,写出∠B的四个三角函数的值.分析 根据正切函数,可得BC与AC的关系,根据锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,可得答案.
解答 解:cotB=tanA=$\frac{BC}{AC}$=20,BC=20AC,
由勾股定理,得
AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{401}$AC,
cosB=sinA=$\frac{BC}{AB}$=$\frac{20AC}{\sqrt{401}AC}$=$\frac{20\sqrt{401}}{401}$,
sinB=cosA=$\frac{AC}{AB}$=$\frac{AC}{\sqrt{401}AC}$=$\frac{\sqrt{401}}{401}$,
tanB=cotA=$\frac{AC}{CB}$=$\frac{AC}{20AC}$=$\frac{1}{20}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知菱形的周长是16,一边上的高是6,则菱形的面积是( )
| A. | 12 | B. | 24 | C. | 48 | D. | 64 |
13.已知一次函数y=kx+b的图象与直线y=-x+1平行,且过点(1,-2),那么此一次函数的解析式为( )
| A. | y=-x+1 | B. | y=x-1 | C. | y=x+2 | D. | y=-x-1 |
 如图,在△ABC中,BC边上的高为AD,AC边上的高为BE,BC=8,AD=5,AC=6,求BE的长.
如图,在△ABC中,BC边上的高为AD,AC边上的高为BE,BC=8,AD=5,AC=6,求BE的长. 如图,点H为△ABC的三条高线的交点,点D在△BCH的外接圆上,且AD⊥BD于点D,延长AD交HC于点P,交外接圆于点E.求证:点P为CH的中点.
如图,点H为△ABC的三条高线的交点,点D在△BCH的外接圆上,且AD⊥BD于点D,延长AD交HC于点P,交外接圆于点E.求证:点P为CH的中点.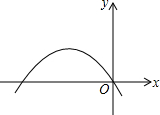 如图的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是-1,抛物线对称轴为直线x=-$\frac{3}{4}$,顶点是(-$\frac{3}{4}$,$\frac{9}{16}$).
如图的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是-1,抛物线对称轴为直线x=-$\frac{3}{4}$,顶点是(-$\frac{3}{4}$,$\frac{9}{16}$).