题目内容
5.已知抛物线y=2x2-4mx+m2的顶点D在直线y=4x+4上.(1)求顶点D的坐标;
(2)设抛物线与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,试求四边形DACB的面积.
分析 (1)根据二次函数顶点坐标公式求出用m表示的顶点坐标,代入直线y=4x+4,求出m的值即可;
(2)求出抛物线与x轴、y轴的交点坐标,然后求四边形DACB的面积.
解答 解:(1)∵y=2x2-4mx+m2,
∴-$\frac{b}{2a}$=-$\frac{-4m}{4}$=m,$\frac{4ac-{b}^{2}}{4a}$=$\frac{8{m}^{2}-16{m}^{2}}{8}$=-m2,
∴D(m,-m2),
将D点坐标代入直线y=4x+4,得
m2+4m+4=0,
解得m=-2,
∴D(-2,-4);
(2)∵m=-2,
∴y=2x2+8x+4,
令y=0,得2x2+8x+4=0,解得x1=-2+$\sqrt{2}$,x2=-2-$\sqrt{2}$,
∴A(-2-$\sqrt{2}$,0),B(-2+$\sqrt{2}$,0),
∴AB=2$\sqrt{2}$,
当x=0时,y=4,
∴C(0,4),
∴S四边形DACB=S△ABC+S△ABD=$\frac{1}{2}$×2$\sqrt{2}$×4+$\frac{1}{2}$×2$\sqrt{2}$×4=8$\sqrt{2}$.
点评 本题主要考查了抛物线与坐标轴的交点,顶点坐标以及待定系数法,根据待定系数法求出m的值是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.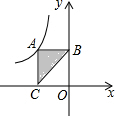 如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
 如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )
如图,点A是反比例函数y=-$\frac{6}{x}$(x<0)的图象上一点,AB⊥y轴于B,点C是x轴上任意一点,则S△ABC等于( )| A. | 12 | B. | 6 | C. | 3 | D. | $\frac{3}{2}$ |
14.下列命题中是真命题的是( )
| A. | 三角形的外角大于它的内角 | |
| B. | 两条边及一个角对应相等的两三角形全等 | |
| C. | 同位角的平分线互相平行 | |
| D. | 位以图形一定是相似图形 |
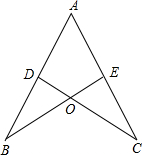 如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O. 如图,BE是△ABC中∠ABC的平分线,DE∥BC,若AE=4,AD=5,EC=3,求DE的长.
如图,BE是△ABC中∠ABC的平分线,DE∥BC,若AE=4,AD=5,EC=3,求DE的长. 如图,方格纸中△ABC的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,则在图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是4个.
如图,方格纸中△ABC的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,则在图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是4个. 如图,在△ABC中,点D、E分别为边AC、AB上的点,且∠ADE=∠B,AE=3,BE=4,则AD•AC=21.
如图,在△ABC中,点D、E分别为边AC、AB上的点,且∠ADE=∠B,AE=3,BE=4,则AD•AC=21.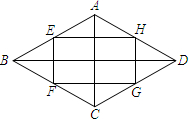 如图,顺次连接菱形ABCD的各边中点E,F,G,H,若AC=6,BD=12,则四边形EFGH的面积为18.
如图,顺次连接菱形ABCD的各边中点E,F,G,H,若AC=6,BD=12,则四边形EFGH的面积为18.