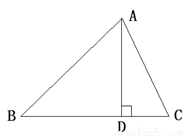
题目内容
5.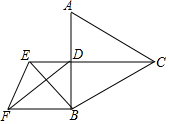 如图,等边三角形ABC的边长为8,CD⊥AB于点D,E为射线CD上一点,以BE为边在BE左侧作等边三角形BEF,求DF的最小值.
如图,等边三角形ABC的边长为8,CD⊥AB于点D,E为射线CD上一点,以BE为边在BE左侧作等边三角形BEF,求DF的最小值.
分析 首先证明△CBE≌△ABF,推出∠BAF=∠BCE,由CA=CB,CD⊥AB,推出∠BCE=$\frac{1}{2}$∠ACB=30°,AD=BD=4,推出∠BAF=30°=定值,根据垂线段最短可知,当DF⊥AF时,DF的值最小.
解答 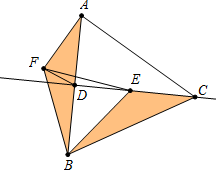 解:如图,∵△ABC,△BEF的是等边三角形,
解:如图,∵△ABC,△BEF的是等边三角形,
∴AB=BC,BF=BE,∠ABC=∠ACB=∠EBF=60°,
∴∠CBE=∠ABF,
在△BCE和△BAF中,
$\left\{\begin{array}{l}{BC=BA}\\{∠CBF=∠ABF}\\{BE=BF}\end{array}\right.$
∴△CBE≌△ABF,
∴∠BAF=∠BCE,
∵CA=CB,CD⊥AB,
∴∠BCE=$\frac{1}{2}$∠ACB=30°,AD=BD=4,
∴∠BAF=30°=定值,
∴根据垂线段最短可知,当DF⊥AF时,DF的值最小,
∴DF的最小值=$\frac{1}{2}$AD=2.
点评 本题考查全等三角形的判定和性质、等边三角形的性质.垂线段最短等知识,解题的关键是利用全等三角形的性质判断出∠FAD=30°=定值,属于中考常考题型.

练习册系列答案
相关题目
16.钓鱼岛面积约4400000平方米,数据4400000用科学记数法表示为( )
| A. | 4.4×106 | B. | 0.44×105 | C. | 44×105 | D. | 4.4×105 |
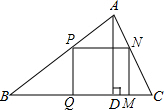 如图,△ABC是一块锐角三角形余料,边BC=12厘米,高AD=8厘米,要把它加工成矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上
如图,△ABC是一块锐角三角形余料,边BC=12厘米,高AD=8厘米,要把它加工成矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上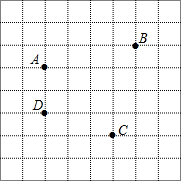 如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母. 如图,在矩形ABCD中,AB=2,∠ADB=30°,沿对角线BD折叠,使△ABD和△EBD落在同一平面内,则A,E之间的距离为2.
如图,在矩形ABCD中,AB=2,∠ADB=30°,沿对角线BD折叠,使△ABD和△EBD落在同一平面内,则A,E之间的距离为2.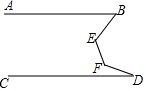 如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.
如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.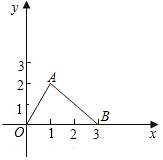 如图,在平面直角坐标系中,点A在第一象限,点A的横坐标为1,OA=2,求点A的坐标.
如图,在平面直角坐标系中,点A在第一象限,点A的横坐标为1,OA=2,求点A的坐标. 已知AB是⊙O的弦,点C为圆上一点.
已知AB是⊙O的弦,点C为圆上一点.