已知二次函数y=x2+ax+a-2.求证:不论a为何实数.此函数图象与x轴总有两个交点．题目和参考答案——青夏教育精英家教网—

题目内容

17．已知二次函数y=x²+ax+a-2，求证：不论a为何实数，此函数图象与x轴总有两个交点．

分析令x²+ax+a-2=0，求出△的值，再判断出其符号即可．

解答证明：令x²+ax+a-2=0，
∵△=a²-4（a-2）=a²-4a+8=（a-2）²+4＞0，
∴不论a为何实数，此函数图象与x轴总有两个交点．

点评本题考查的是抛物线与x轴的交点，熟知二次函数y=ax²+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax²+bx+c=0根之间的关系是解答此题的关键．

练习册系列答案

小学升学多轮夯基总复习系列答案

金钥匙期末冲刺100分系列答案

名师指导期末冲刺卷系列答案

初中英语听力训练苏州大学出版社系列答案

相关题目

a³+a³=a⁶

x²•x³=x⁶

（-2xy²）³=-8x³y⁶

$（-\frac{1}{2}）^{2}=-\frac{1}{4}$

B．

3a^-2=$\frac{1}{3{a}^{2}}$

0⁰=1

12．

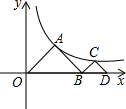如图所示，点A、C都是双曲线y=$\frac{4}{x}$在第一象限分支上的点，且△AOB和△BCD都是等腰直角三角形，∠A=∠C=90°，求点D的坐标．

2．已知m是-2的相反数，n是-1的倒数，则（m+n）²⁰¹⁶=1．

9．已知点A（3，y₁），B（2，y₂）在二次函数y=（x-1）²+1的图象上，则y₁＞y₂．

6．已知Q是圆内接四边形ABCD的对角线的交点，PB、PD是圆的切线，且P在直线AC上，求证：（1）$\frac{QA}{OC}$=$\frac{AB•AD}{CB•CD}$；（2）$\frac{QA}{QC}$=$\frac{PA}{PC}$．

7．-$\frac{1}{2016}$的相反数是（　　）

试题分类