题目内容
13.若抛物线y=$\frac{1}{2}$x2+x+c与x轴没有交点,则直线y=cx+1经过一、二、三象限.分析 由抛物线y=$\frac{1}{2}$x2+x+c与x轴没有交点可知:△<0,从而可求得c的取值范围,然后根据一次函数的性质可判断出直线经过的象限.
解答 解:∵抛物线y=$\frac{1}{2}$x2+x+c与x轴没有交点,
∴△<0,即12-4×$\frac{1}{2}$×c<0.
解得:c$>\frac{1}{2}$.
∵c>0,
∴直线y=cx+1经过一、二、三象限.
故答案为:一、二、三.
点评 本题主要考查的是抛物线与x轴的交点、一次函数的图象和性质,确定出c的取值范围是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.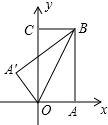 如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )
如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )
 如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )
如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=$\sqrt{5}$,$\frac{BC}{OC}=\frac{1}{2}$,则点A′的坐标( )| A. | $(-\frac{3}{5},\frac{4}{5})$ | B. | $(-\frac{2}{5},\frac{4}{5})$ | C. | $(-\frac{4}{5},\frac{3}{5})$ | D. | $(-\frac{2}{5},\frac{3}{5})$ |
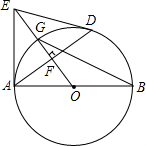 如图,AB是⊙O的直径,D是⊙O上一点,OF⊥AD,过点A作⊙O的切线,交OF的延长线于E.连接DE,DE与⊙O相切,若AE=10,sin∠AEO=$\frac{3}{5}$,求BG长.
如图,AB是⊙O的直径,D是⊙O上一点,OF⊥AD,过点A作⊙O的切线,交OF的延长线于E.连接DE,DE与⊙O相切,若AE=10,sin∠AEO=$\frac{3}{5}$,求BG长. 已知:如图,△ABC≌△DEF,BC=8cm,EC=5cm,求线段CF的长.
已知:如图,△ABC≌△DEF,BC=8cm,EC=5cm,求线段CF的长.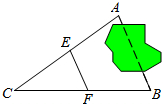 如图,要测量的A,B两点被池塘隔开,李师傅在AB外任选一点C,连结CA,CB,分别取CA,CB的中点E、F,量得E,F两点间的距离等于12.5米,则A、C两点间的距离是25米.
如图,要测量的A,B两点被池塘隔开,李师傅在AB外任选一点C,连结CA,CB,分别取CA,CB的中点E、F,量得E,F两点间的距离等于12.5米,则A、C两点间的距离是25米.