题目内容
1.观察下面各式的规律:12+(1×2)2+22=(1×2+1)2
22+(2×3)2+32=(2×3+1)2
32+(3×4)2+42=(3×4+1)2
…
(1)写出第2015个式子;
(2)写出第n个式子,并验证你的结论.
分析 (1)仿照已知式子得出第2015个式子即可;
(2)以此类推得出第n个式子即可.
解答 解:(1)根据题意得:第2015个式子为20152+(2015×2016)2+20162=(2015×2016+1)2;
(2)以此类推,第n行式子为n2+[n(n+1)]2+(n+1)2=[n(n+1)+1]2.
证明:左边=n2+(n2+n)2+(n+1)2=n4+2n3+3 n2+2n+1
右边=(n2+n+1)2=n4+2n3+3 n2+2n+1
所以n2+[n•(n+1)]2+(n+1)2=[n•(n+1)+1]2
点评 此题考查了完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
9.|1-$\sqrt{2}$|的相反数为( )
| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 1+$\sqrt{2}$ | D. | -1-$\sqrt{2}$ |
13. 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
 如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )| A. | 2.4cm | B. | 4.8cm | C. | 5cm | D. | 9.6cm |
11. 如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )
如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )
 如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )
如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )| A. | 25° | B. | 35° | C. | 55° | D. | 65° |
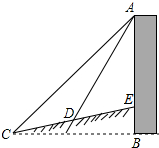 重庆建筑多因地制宜、依山而建,现有以住宅楼如图所示,该楼背后为一斜坡,坡角为15°,为测得该楼的高度,一兴趣小组的同学在C点测得楼顶A点的仰角为45°,点D点测的仰角为60°,CD两点之间的距离是20米,C、B在同一水平地面上,CD与AB交于点E.
重庆建筑多因地制宜、依山而建,现有以住宅楼如图所示,该楼背后为一斜坡,坡角为15°,为测得该楼的高度,一兴趣小组的同学在C点测得楼顶A点的仰角为45°,点D点测的仰角为60°,CD两点之间的距离是20米,C、B在同一水平地面上,CD与AB交于点E.