题目内容
16.某中学为了预测本校应届毕业生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图所示的部分频数分布直方图(从左到右依次为第一到第六小组,每小组含最小值,不含最大值)和扇形统计图,请根据统计图中提供的信息解答下列问题:(1)本次抽取的女生总人数为50人,其中第四小组的人数为10,第六小组人数占总人数的百分比为8%;
(2)请补全频数分布直方图:
(3)若“一分钟跳绳”不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数:
(4)若“一分钟跳绳”成绩不低于170次的为满分,不低于130次的为优秀,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?

分析 (1)根据第二组的人数是10,所占的百分比是20%即可求得总人数,然后根据百分比的意义求解;
(2)根据(1)的结果即可补全直方图;
(3)利用总人数260乘以对应的百分比即可求解;
(4)利用概率公式即可直接求解.
解答 解:(1)总人数是:10÷20%=50(人),
第四小组的人数为:50-4-10-16-6-4=10(人),
第六小组人数占总人数的百分比是:$\frac{4}{50}$×100%=8%.
故答案是:50人;10;8%;
(2)如图:
(3)“一分钟跳绳”成绩的优秀人数为
260×$\frac{20}{50}$=104(人);
(4)成绩为满分的概率为$\frac{4}{20}$=$\frac{1}{5}$.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
相关题目
11.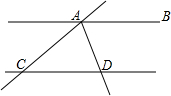 如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
 如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
8. 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )| A. | $\frac{9}{2}$ | B. | $\frac{27}{4}$ | C. | $\frac{24}{5}$ | D. | 12 |
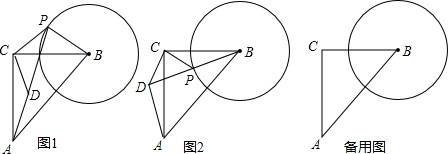
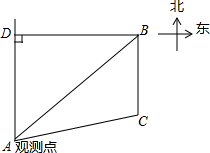 已知B村庄位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为24km,一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此摩托车与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,$\sqrt{2}$≈1.41,$\sqrt{5}$≈2.24.
已知B村庄位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为24km,一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此摩托车与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,$\sqrt{2}$≈1.41,$\sqrt{5}$≈2.24.