题目内容
12.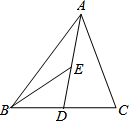 如图,在△ABC中,D,E分别是BC、AD的中点,S△ABC=4,则S△ABE=( )
如图,在△ABC中,D,E分别是BC、AD的中点,S△ABC=4,则S△ABE=( )| A. | 2 | B. | 1 | C. | 0.5 | D. | 0.25 |
分析 由图可知S△ABD和S△ABD等底等高,所以S△ABD=$\frac{1}{2}$S△ABC,同理可得S△ABE=$\frac{1}{2}$S△ABD,代入即可求出.
解答 解:∵△ABC中,D是BC中点,
∴S△ABD=$\frac{1}{2}$S△ABC,
又∵E是AD的中点,
∴S△ABE=$\frac{1}{2}$S△ABD,
∴S△ABE=$\frac{1}{4}$S△ABC,
∵S△ABC=4,
∴S△ABE=1.
故选B.
点评 本题考查了三角形的面积的等积变换,熟练找出相关联的底、高是解答本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
20.在直线l上有三点B、C、D,直线l外有一点A,若AB=10cm,AC=11cm,AD=7cm,那么A点到直线的距离( )
| A. | 等于7cm | B. | 等于10cm | ||
| C. | 不大于7cm | D. | 大于7cm而小于11cm |
7.线段AB=3,且AB∥x轴,若A(-2,4),则将线段向下平移4个单位长度后,点B的对应点的坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (-5,1) | D. | (1,0)或(-5,0) |
4.下列是二元一次方程的是( )
| A. | 3x=10 | B. | 2x2=y | C. | y+$\frac{1}{x}$=2 | D. | x+8y=0 |
19.下列各等式成立的是( )
| A. | $\frac{n}{n-m}$=-$\frac{n}{m+n}$ | B. | $\frac{n}{m-n}$=-$\frac{n}{m+n}$ | C. | $\frac{n}{n-m}$=-$\frac{-n}{m+n}$ | D. | $\frac{n}{n-m}$=-$\frac{n}{m-n}$ |
 按要求分别解这个方程:①配方法;②因式分解法.
按要求分别解这个方程:①配方法;②因式分解法.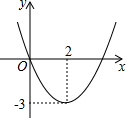 某同学从图中(二次函数y=ax2+bx+c)观察得出下面五条信息①a<0,②c=0,③函数的最小值为-3,④当x<0时,y>0,⑤函数的对称轴为x=2,你认为其中正确的有:②③④⑤(填出序号)
某同学从图中(二次函数y=ax2+bx+c)观察得出下面五条信息①a<0,②c=0,③函数的最小值为-3,④当x<0时,y>0,⑤函数的对称轴为x=2,你认为其中正确的有:②③④⑤(填出序号) 表示(其中,n≥1).这是用无理数表示有理数的一个范例.
表示(其中,n≥1).这是用无理数表示有理数的一个范例.