题目内容
19．
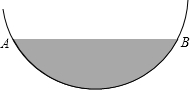某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．（1）请你补全这个输水管道的圆形截面；
（2）若这个输水管道有水部分的水面宽AB=12cm，水面最深地方的高度为2cm，求这个圆形截面所在圆的半径．
分析 （1）先作弦AB的垂直平分线；在弧AB上任取一点C连接AC，作弦AC的垂直平分线，两线交点作为圆心O，OA作为半径，画圆即可；
（2）过O作OE⊥AB于D，交弧AB于E，连接OB．根据垂径定理得到BD=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6cm，然后根据勾股定理列出关于圆形截面半径的方程求解．
解答 解：（1）先作弦AB的垂直平分线；在弧AB上任取一点C连接AC，作弦AC的垂直平分线，两线交点作为圆心O，OA作为半径，画圆即为所求图形．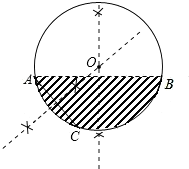
（2）过O作OE⊥AB于D，交弧AB于E，连接OB．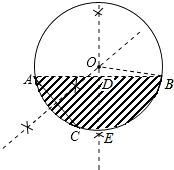
∵OE⊥AB，
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6cm，
由题意可知，ED=2cm，
设半径为xcm，则OD=（x-2）cm，
在Rt△BOD中，由勾股定理得：OD2+BD2=OB2
∴（x-2）2+62=x2
解得x=10，
即这个圆形截面的半径为10cm．
点评 本题主要考查了垂径定理、勾股定理的运用．解决问题的关键是根据题意画出图形，再根据勾股定理进行求解．
练习册系列答案
相关题目
4．
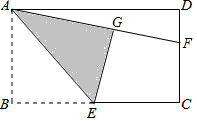如图，在矩形ABCD中，E是BC边的中点，将△ABE沿AE所在直线折叠得到△AGE，延长AG交CD于点F，已知CF=2，FD=1，则BC的长是（ ）
如图，在矩形ABCD中，E是BC边的中点，将△ABE沿AE所在直线折叠得到△AGE，延长AG交CD于点F，已知CF=2，FD=1，则BC的长是（ ）| A． | 3$\sqrt{2}$ | B． | 2$\sqrt{6}$ | C． | 2$\sqrt{5}$ | D． | 2$\sqrt{3}$ |
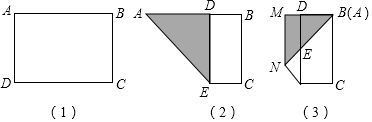
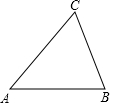如图有一张面积为10的三角形ABC纸片，其中AB为5，把它剪两刀拼成一个矩形（无缝隙、无重叠），且矩形的一边与AB平行，则矩形的周长为14或10．
如图，方格是由边长为1个单位长度的正方形组成的．
如图①所示是一个长为2a，宽为2b的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．