题目内容
14.如图,将一张长方形纸片ABCD如图(1)折叠,使AD边落在AB边上,折痕为AE,如图(2):再将∠A折叠,使点A与点B重合,折痕为MN,如图(3).如果AD=6cm,MD=1cm,那么长方形ABCD原来的长AB=10cm.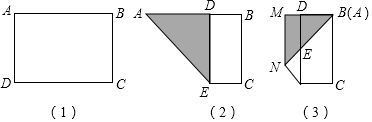
分析 利用折叠的性质,可得BM=$\frac{1}{2}$AB=$\frac{1}{2}$(AD+BD)=BD+MD,由此代入数值即可求得BD的长,继而求得答案.
解答 解:由折叠可知:BM=$\frac{1}{2}$AB=$\frac{1}{2}$(AD+BD)=BD+MD,
又∵AD=6cm,MD=1cm,
∴$\frac{1}{2}$(6+BD)=BD+1,
解得:BD=4cm,
∴AB=AD+BD=10cm.
故答案为:10.
点评 此题考查了折叠的性质以及矩形的性质.注意得到BM=$\frac{1}{2}$AB=$\frac{1}{2}$(AD+BD)=BD+MD是关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
2.方程2x2-3x-1=0用公式法求解,先确定a,b,c的值,正确的是( )
| A. | a=2,b=-3,c=-1 | B. | a=-2,b=3,c=1 | C. | a=-2,b=-3,c=-1 | D. | a=2,b=3,c=-1 |
6.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{\frac{1}{3}}$ |
3.下列代数式书写规范的是( )
| A. | 1$\frac{1}{6}$a | B. | a×5 | C. | a÷b | D. | $\frac{1}{3}ab$ |
4.观察下表:
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为9x+4y,第3格的“特征多项式”为12x+6y;
(2)写出第5格的“特征多项式”与第6格的“特征多项式”,并求出第5格与第6格
“特征多项式”的差.
(3)试写出第n格的“特征多项式”.
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
(1)第2格的“特征多项式”为9x+4y,第3格的“特征多项式”为12x+6y;
(2)写出第5格的“特征多项式”与第6格的“特征多项式”,并求出第5格与第6格
“特征多项式”的差.
(3)试写出第n格的“特征多项式”.
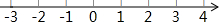 解不等式组$\left\{\begin{array}{l}3x-3≥x-7\\ \frac{2x+4}{3}<3-x\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}3x-3≥x-7\\ \frac{2x+4}{3}<3-x\end{array}\right.$,并把解集在数轴上表示出来.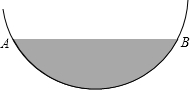 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.