题目内容
13.如果关于x的方程x2+kx+$\frac{1}{2}$k2+$\frac{1}{2}$k+$\frac{1}{4}$=0有两个实数根x1、x2,那么$\frac{{x}_{1}^{2016}}{{x}_{2}^{2015}}$的值为-$\frac{1}{2}$.分析 根据题意可得△=b2-4ac≥0,求得k=-1,于是原方程为x2-x+$\frac{1}{4}$=0,列方程得到x1=x2=-$\frac{1}{2}$,于是得到结论.
解答 解:根据题意可得
∵方程有实数根,
∴△=b2-4ac≥0,
即k2-4($\frac{1}{2}$k2+$\frac{1}{2}$k+$\frac{1}{4}$)≥0,
∴-(k+1)2≥0,
∵(k+1)2≤0,
∴k+1=0,
即k=-1,
∴原方程为:x2-x+$\frac{1}{4}$=0,
∴x1=x2=-$\frac{1}{2}$,
∴$\frac{{x}_{1}^{2016}}{{x}_{2}^{2015}}$=x1=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查了根的判别式、根与系数的关系、解方程,解题的关键是根据根的判别式先求出k.

练习册系列答案
相关题目
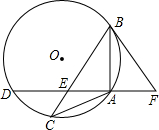 已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.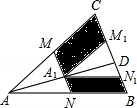 如图,如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置,且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为14.
如图,如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置,且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为14.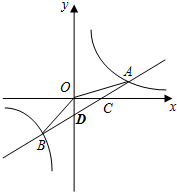 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B的坐标为(m,-2).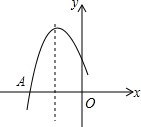 二次函数y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2<4ac;②2a+b=0;③a+b+c=0;④若点B(-$\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上得两点,则y1=y2;其中正确结论是( )
二次函数y=ax2+bx+c图象的一部分如图所示,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2<4ac;②2a+b=0;③a+b+c=0;④若点B(-$\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上得两点,则y1=y2;其中正确结论是( )