题目内容
已知AO⊥BO,OB<OA<2OB,在AO上取一点C使AC=BO,在BO上取一点D使BD=CO,连接AD、BC交于P.求证:∠APC=45°.
考点:全等三角形的判定与性质,平行四边形的判定与性质
专题:证明题
分析:作BE⊥OB,且BE=BO,连接DE交BC于Q,如图,先利用“SAS”证明△BOC≌△EBD,则∠2=∠1,BC=DE,易得∠1+∠3=90°,则∠BQE=90°,由于AC=OB,而BE=BO,则AC=BE,而AC∥BE,于是可证明四边形ACBE为平行四边形,则AE∥BC,AE=BC,根据平行线的性质得∠AED=∠BQE=90°,AE=DE,则△AED为等腰直角三角形,得到∠EAD=45°,然后根据平行线的性质即可得到∠APC=∠EAD=45°.
解答:证明:作BE⊥OB,且BE=BO,连接DE交BC于Q,如图,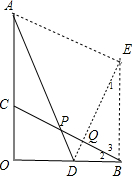
∵AO⊥BO,BE⊥BC,
∴∠COB=∠DBE=90°,
在△BOC和△EBD中,
,
∴△BOC≌△EBD(SAS),
∴∠2=∠1,BC=DE,
而∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠BQE=90°,
∵AC=OB,
而BE=BO,
∴AC=BE,
∵AO⊥BO,BE⊥BC,
∴AC∥BE,
∴四边形ACBE为平行四边形,
∴AE∥BC,AE=BC
∴∠AED=∠BQE=90°,AE=DE,
∴△AED为等腰直角三角形,
∴∠EAD=45°,
∴∠APC=∠EAD=45°.

∵AO⊥BO,BE⊥BC,
∴∠COB=∠DBE=90°,
在△BOC和△EBD中,
|
∴△BOC≌△EBD(SAS),
∴∠2=∠1,BC=DE,
而∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠BQE=90°,
∵AC=OB,
而BE=BO,
∴AC=BE,
∵AO⊥BO,BE⊥BC,
∴AC∥BE,
∴四边形ACBE为平行四边形,
∴AE∥BC,AE=BC
∴∠AED=∠BQE=90°,AE=DE,
∴△AED为等腰直角三角形,
∴∠EAD=45°,
∴∠APC=∠EAD=45°.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了平行四边形的判定与性质.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
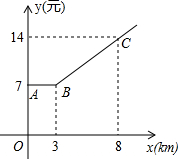 如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
 如图,在?ABCD中,AC与BD交于点O,若AB=8,BC=6,△AOD的周长是16,则△AOB的周长等于
如图,在?ABCD中,AC与BD交于点O,若AB=8,BC=6,△AOD的周长是16,则△AOB的周长等于