Question

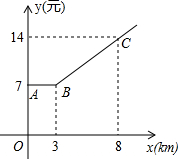如图，折线ABC是在某市乘出租车所付车费y（元）与行车里程x（km）之间的函数关系图象．
①根据图象，求当x≥3时的函数关系式；
②某人乘坐2.5km，应付多少钱？
③某人乘坐13km，应付多少钱？
④若某人付车费30.8元，出租车行驶了多少路程？

Answer 1

考点：一次函数的应用

专题：

分析：①设x≥3时的函数关系式为y=kx+b（k≠0），然后利用待定系数法求一次函数解析式解答；
②根据x＜3时，付费都是7元解答；
③把x=13代入函数关系式计算即可得解；
④把y=30.8代入函数关系式解方程即可．

解答：解：①设x≥3时的函数关系式为y=kx+b（k≠0），
∵函数图象经过点（3，7），（8，14），
∴

3k+b=7 8k+b=14

，
解得

k=1.4 b=2.8

．
∴函数关系式为y=1.4x+2.8；

②x=2.5时，y=7元；

③x=13时，y=1.4×13+2.8=18.2+2.8=21元；

④y=30.8时，1.4x+2.8=30.8，
解得x=20．
答：某人付车费30.8元，出租车行驶了20km路程．

点评：本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，已知自变量求函数值，已知函数值求自变量，待定系数法求函数解析式是常用的方法，需熟练掌握．