题目内容
10．
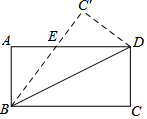如图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C'处，BC'交AD于点E，则线段AE的长为（ ）| A． | $\frac{9}{4}$ | B． | 3 | C． | $\frac{15}{4}$ | D． | $\frac{15}{2}$ |
分析 首先根据题意得到BE=DE，然后根据勾股定理得到关于线段AB、AE、BE的方程，解方程求出ED，即可得出AE的长．
解答 解：设ED=x，则AE=6-x，
∵四边形ABCD为矩形，
∴AD∥BC，AD=BC=6，AB=CD=3，
∴∠EDB=∠DBC；
由题意得：∠EBD=∠DBC，
∴∠EDB=∠EBD，
∴EB=ED=x；
由勾股定理得：
BE2=AB2+AE2，
即x2=9+（6-x）2，
解得：x=$\frac{15}{4}$，
∴ED=$\frac{15}{4}$．
∴AE=AD-ED=6-$\frac{15}{4}$=$\frac{9}{4}$
故选：A．
点评 本题主要考查了几何变换中的翻折变换、矩形的性质、勾股定理；熟练掌握翻折变换和矩形的性质，由勾股定理得出方程是关键．
练习册系列答案
阅读快车系列答案
相关题目
1．
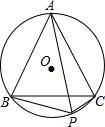如图，等边△ABC是⊙O的内接三角形，P是$\widehat{BC}$上一点，当PB=3PC时，则△ABC与四边形ABPC的面积比为（ ）
如图，等边△ABC是⊙O的内接三角形，P是$\widehat{BC}$上一点，当PB=3PC时，则△ABC与四边形ABPC的面积比为（ ）| A． | $\frac{13}{16}$ | B． | $\frac{10}{13}$ | C． | $\frac{9}{11}$ | D． | $\frac{7}{9}$ |
18．
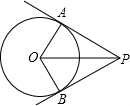如图，PA，PB是⊙O的两条切线，切点分别是A，B，如果OP=4，PA=2$\sqrt{3}$，那么∠APB等于（ ）
如图，PA，PB是⊙O的两条切线，切点分别是A，B，如果OP=4，PA=2$\sqrt{3}$，那么∠APB等于（ ）| A． | 90° | B． | 100° | C． | 110° | D． | 60° |
如图，是由5个相同的正方体组成的立体图形，从上面观察这个立体图形，得到的平面图形是（ ）
2．下列命题为假命题的是（ ）
| A． | 有两边及一角对应相等的两个三角形全等 | |
| B． | 面积之比为1：4的两个相似三角形的周长之比是1：2 | |
| C． | 方程x2-x-2=0有两个不相等的实数根 | |
| D． | 顺次连接任意四边形各边中点得到的四边形是平行四边形 |
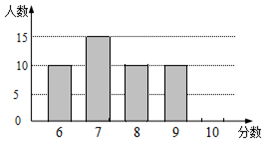某校组织开展校园诗词大会，参赛学生均作答10题，每答对一题得1分．随机抽取的九年级50名学生答题分数的情况有如下所示的不完整的条形统计图．