题目内容
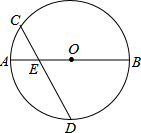 如图,⊙O中,AB是直径,弦CD交AB于E点,且CE=OE,若
如图,⊙O中,AB是直径,弦CD交AB于E点,且CE=OE,若 |
| AC |
 |
| BD |
考点:圆心角、弧、弦的关系
专题:
分析:连接OC,OD,AD,根据圆心角、弧、弦的关系可得出∠AOC=30°,再由CE=OE可知∠C=30°,根据等腰三角形的性质可知∠ODC=∠C=30°,由圆周角定理可得出∠ADB=90°,∠ADC=
∠AOC=15°,故可得出∠ODB的度数,再由三角形内角和定理即可得出结论.
| 1 |
| 2 |
解答: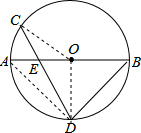 解:连接OC,OD,AD,
解:连接OC,OD,AD,
∵
=30°,
∴∠AOC=30°,
∴∠ADC=
∠AOC=15°.
∵CE=OE,
∴∠C=∠AOC=30°.
∵OC=OD,
∴∠ODC=∠C=30°.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ODB=∠AOB-∠ADC-∠ODC=90°-15°-30°=45°.
∵OD=OB,
∴∠OBD=∠ODB=45°,
∴∠BOD=90°,
∴
=90°.
 解:连接OC,OD,AD,
解:连接OC,OD,AD,∵
 |
| AC |
∴∠AOC=30°,
∴∠ADC=
| 1 |
| 2 |
∵CE=OE,
∴∠C=∠AOC=30°.
∵OC=OD,
∴∠ODC=∠C=30°.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ODB=∠AOB-∠ADC-∠ODC=90°-15°-30°=45°.
∵OD=OB,
∴∠OBD=∠ODB=45°,
∴∠BOD=90°,
∴
 |
| BD |
点评:本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,等边△ABC,AD⊥BC,交BC于点D,BD=5cm,则AC的长为
如图,等边△ABC,AD⊥BC,交BC于点D,BD=5cm,则AC的长为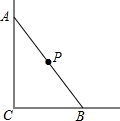 如图所示,一根长为5米的木棍AB,斜靠在与地面垂直的墙上.设木棍的中点为P,若棍子A端沿墙下滑,且B端沿地面向右滑行.请判断木棍滑动的过程中,点P到点C的距离是否发生变化:
如图所示,一根长为5米的木棍AB,斜靠在与地面垂直的墙上.设木棍的中点为P,若棍子A端沿墙下滑,且B端沿地面向右滑行.请判断木棍滑动的过程中,点P到点C的距离是否发生变化: