题目内容
已知关于x的一元二次方程x2+(2k-1)x+k2+1=0有实数根x1、x2,且x12+x22=17,求k的值.
考点:根与系数的关系,根的判别式
专题:
分析:依据根与系数关系,表示出两根的和与两根的积,依据x12+x22=(x1+x2)2-2x1x2,即可得到关于k的方程,即可求得k的值.
解答:解:∵关于x的一元二次方程x2+(2k-1)x+k2+1=0有实数根x1、x2,
∴x1+x2=-(2k-1),x1x2=k2+1,
∵x12+x22=(x1+x2)2-2x1x2=17,
∴[-(2k-1)]2-2(k2+1)=17,
解得:k1=1+
,k2=1-
,
又∵方程x2+(2k-1)x+k2+1=0有两个实数根,
∴△=(2k-1)2-4(k2+1)≥0,
∴k≤-
∴k1=1+
不合题意,舍去;
故符合条件的k的值为1-
.
∴x1+x2=-(2k-1),x1x2=k2+1,
∵x12+x22=(x1+x2)2-2x1x2=17,
∴[-(2k-1)]2-2(k2+1)=17,
解得:k1=1+
| 10 |
| 10 |
又∵方程x2+(2k-1)x+k2+1=0有两个实数根,
∴△=(2k-1)2-4(k2+1)≥0,
∴k≤-
| 3 |
| 4 |
∴k1=1+
| 10 |
故符合条件的k的值为1-
| 10 |
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.通过变形可以得到关于待定系数的方程解决问题.注意满足根与系数的关系定理的前提条件是判别式△≥0.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,AP平分∠BAF,PD⊥AB于点D,PE⊥AF于点E,则△APD与△APE全等的理由是( )
如图,AP平分∠BAF,PD⊥AB于点D,PE⊥AF于点E,则△APD与△APE全等的理由是( )| A、SSS | B、SAS |
| C、SSA | D、AAS |

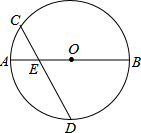 如图,⊙O中,AB是直径,弦CD交AB于E点,且CE=OE,若
如图,⊙O中,AB是直径,弦CD交AB于E点,且CE=OE,若
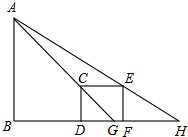 如图,为测量山峰AB的高度,在D处和F处竖立标杆DC和FE,标杆的高都是4米,相隔50米,并且AB、CD和EF在同一平面内,从标杆DC退后2米到G处可以看到山峰和标杆顶点C在同一直线上,从标杆FE退后4米到H处可以看到山峰A和标杆顶端E在同一直线上,求山峰高度AB及其与标杆CD的水平距离BD的长.
如图,为测量山峰AB的高度,在D处和F处竖立标杆DC和FE,标杆的高都是4米,相隔50米,并且AB、CD和EF在同一平面内,从标杆DC退后2米到G处可以看到山峰和标杆顶点C在同一直线上,从标杆FE退后4米到H处可以看到山峰A和标杆顶端E在同一直线上,求山峰高度AB及其与标杆CD的水平距离BD的长.
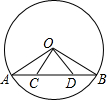 如图,AB是⊙O的一条弦,线段OC、OD交弦AB于点C、D,且AC=BD.求证:OC=OD.
如图,AB是⊙O的一条弦,线段OC、OD交弦AB于点C、D,且AC=BD.求证:OC=OD.